设点 $D$ 是锐角 $\triangle ABC$ 的边 $BC$ 上一点,以线段 $BD$ 为直径的圆分别交 直线 $AB、AD$ 于点 $X、P$(异于点 $B、D$),以线段 $CD$ 为直径的圆分别交直线 $AC、AD$ 于点 $Y、Q$(异于点 $C、D$).过 $B$ 点 $A$ 作直线 $PX、QY$ 的垂线,垂足分 别为 $M、N$.
求证:$\triangle AMN\sim \triangle AB C$ 的充分必要条件是直线 $ AD$ 过 $\triangle ABC$ 的外心.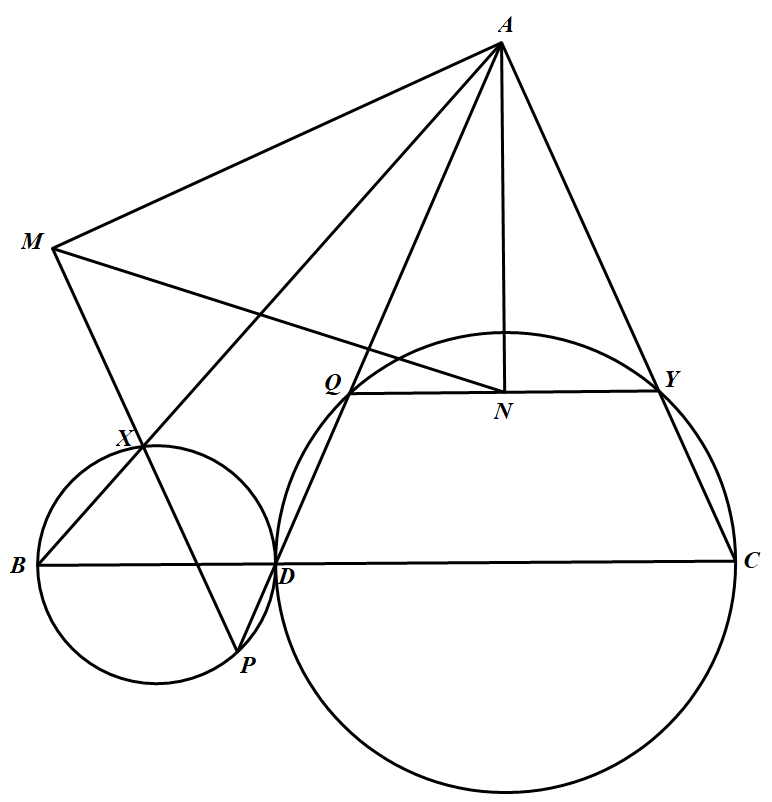
求证:$\triangle AMN\sim \triangle AB C$ 的充分必要条件是直线 $ AD$ 过 $\triangle ABC$ 的外心.

【难度】
【出处】
2009年中国西部数学奥林匹克试题
【标注】
【答案】
略
【解析】
连结 $XY、DX$,由已知有 $B,P,D,X$ 四点共圆,$C,Y, Q, D$ 四点共圆,故 $\angle A X M=\angle B X P=\angle B D P=\angle Q D C=\angle A Y N$.
又因为 $\angle A M X=\angle A N Y=90^{\circ}$,所以 $\triangle A M X \sim \triangle A N Y$,所以 $\angle M A X=\angle N A Y, \dfrac{A M}{A X}=\dfrac{A N}{A Y}$.
从而 $\angle M A N=\angle X A Y$,结合 $\frac{A M}{A X}=\frac{A N}{A Y}$,得 $\triangle A M N \sim \triangle A X Y$.
所以,$\triangle A M N \sim \triangle A B C \Leftrightarrow \triangle A X Y \sim\triangle A B C \Leftrightarrow X Y / / B C \Leftrightarrow\angle X D B=90^{\circ}-\angle A B C$.
而由 $A, X, D, Y$ 四点共圆,知 $\angle D X Y=\angle D A Y$,又 $\angle X D B=90^{\circ}-\angle A B C$,所以 $\angle D X Y=\angle X D B \Leftrightarrow \angle D A C=90^{\circ}-\angle A B C$,等价于直线 $AD$ 过 $\triangle ABC$ 的外心.
所以,$\triangle A M N \sim \triangle A B C$ 的充分必要条件是直线 $AD$ 过 $\triangle ABC$ 的外心.
又因为 $\angle A M X=\angle A N Y=90^{\circ}$,所以 $\triangle A M X \sim \triangle A N Y$,所以 $\angle M A X=\angle N A Y, \dfrac{A M}{A X}=\dfrac{A N}{A Y}$.
从而 $\angle M A N=\angle X A Y$,结合 $\frac{A M}{A X}=\frac{A N}{A Y}$,得 $\triangle A M N \sim \triangle A X Y$.
所以,$\triangle A M N \sim \triangle A B C \Leftrightarrow \triangle A X Y \sim\triangle A B C \Leftrightarrow X Y / / B C \Leftrightarrow\angle X D B=90^{\circ}-\angle A B C$.
而由 $A, X, D, Y$ 四点共圆,知 $\angle D X Y=\angle D A Y$,又 $\angle X D B=90^{\circ}-\angle A B C$,所以 $\angle D X Y=\angle X D B \Leftrightarrow \angle D A C=90^{\circ}-\angle A B C$,等价于直线 $AD$ 过 $\triangle ABC$ 的外心.
所以,$\triangle A M N \sim \triangle A B C$ 的充分必要条件是直线 $AD$ 过 $\triangle ABC$ 的外心.
答案
解析
备注