如图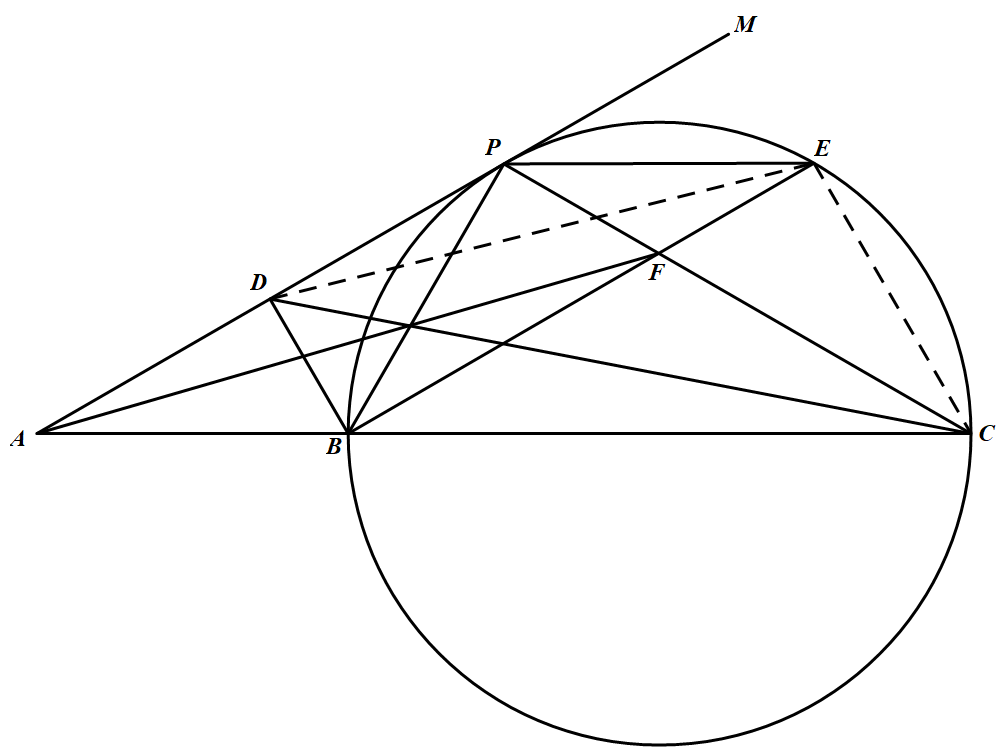
在 $\triangle PBC$ 中，$\angle PBC = 60^\circ$，过点 $P$ 作 $\triangle PBC$ 的外接圆 $\omega$ 的切线，与 $CB$ 的延长线交于点 $A$．点 $D$ 和 $E$ 分别在线段 $PA$ 和圆 $\omega$ 上，使得 $\angle D B E=90^{\circ}, P D=P E$．连接 $BE$，与 $PC$ 相交于点 $F$．已知 $AF、BP、CD$ 三线共点．
（1）求证：$BF$ 是 $\angle PBC$ 的角平分线；
（2）求 $\tan\angle PCB$ 的值．
在 $\triangle PBC$ 中，$\angle PBC = 60^\circ$，过点 $P$ 作 $\triangle PBC$ 的外接圆 $\omega$ 的切线，与 $CB$ 的延长线交于点 $A$．点 $D$ 和 $E$ 分别在线段 $PA$ 和圆 $\omega$ 上，使得 $\angle D B E=90^{\circ}, P D=P E$．连接 $BE$，与 $PC$ 相交于点 $F$．已知 $AF、BP、CD$ 三线共点．（1）求证：$BF$ 是 $\angle PBC$ 的角平分线；
（2）求 $\tan\angle PCB$ 的值．
【难度】
【出处】
2006年中国西部数学奥林匹克试题
【标注】
【答案】
略
【解析】
（1）当 $BF$ 平分 $\angle PBC$ 时，由与 $\angle DBE=90^\circ$，所以，$BD$ 平分 $\angle PEA$，于是 $\dfrac{P F}{F C} \cdot \dfrac{C B}{B A} \cdot \dfrac{A D}{D P}=\dfrac{P B}{B C} \cdot \dfrac{B C}{B A} \cdot \dfrac{A B}{P B}=1$．所以，由Ceva定理的逆定理知，$AF、BP、CD$ 三线共点．
若还有一个角 $\angle D^{\prime} B F^{\prime}$ 满足 $\angle D^{\prime} B F^{\prime}=90^{\circ}$，且 $AF^\prime、BP、CD^\prime$ 三线共点，不妨设 $F^\prime$ 在线段 $PF$ 内，则 $D^\prime$ 在线段 $AD$ 内，于是 $\dfrac{P F^{\prime}}{F^{\prime} C}<\dfrac{P F}{F C}, \dfrac{A D^{\prime}}{P D^\prime}<\dfrac{A D}{P D}$，所以 $\dfrac{P F^{\prime}}{F^{\prime} C} \cdot \dfrac{C B}{B A} \cdot \dfrac{A D^{\prime}}{D^{\prime} P}<\dfrac{P F}{F C} \cdot \dfrac{C B}{B A} \cdot \dfrac{A D}{P D}=1$．这与 $A F^{\prime}, B P, C D^{\prime}$ 三线共点矛盾．
所以，$BF$ 是 $\angle PBC$ 的内角平分线．
（2）不妨设圆 $O$ 的半径为 $1$，$\angle P C B=\alpha$，由（1）知，$\angle P B E=\angle E B C=30^{\circ}$，$E$ 是 $\overparen{PC}$ 的中点．因为 $\angle M P E=\angle P B E=30^{\circ}, \angle C P E=\angle C B E=30^{\circ}$，所以由 $PD=PE$ 知，$\angle P D E=\angle P E D=15^{\circ}$，$P E=2 \cdot 1 \cdot \sin 30^{\circ}=1, D E=2 \cos 15^{\circ}$．
又 $B E=2 \sin \angle E C B=2 \sin \left(\alpha+30^{\circ}\right), \angle B E D=\angle B E P-15^{\circ}=\alpha-15^{\circ}$，所以，在直角三角形 $BDE$ 中，有
$\cos \left(\alpha-15^{\circ}\right)=\dfrac{B E}{D E}=\dfrac{2 \sin \left(\alpha+30^{\circ}\right)}{2 \cos 15^{\circ}}$
$\cos \left(\alpha-15^{\circ}\right) \cos 15^{\circ}=\sin \left(\alpha+30^{\circ}\right)$
$\cos \alpha+\cos \left(\alpha-30^{\circ}\right)=2 \sin \left(\alpha+30^{\circ}\right)$
$\cos \alpha+\cos \alpha \cos 30^{\circ}+\sin \alpha \sin 30^{\circ}=\sqrt{3} \sin \alpha+\cos \alpha$
$1+\dfrac{\sqrt{3}}{2}+\dfrac{1}{2} \tan \alpha=\sqrt{3} \tan \alpha+1$
所以 $\tan \alpha=\dfrac{6+\sqrt{3}}{11}$．
若还有一个角 $\angle D^{\prime} B F^{\prime}$ 满足 $\angle D^{\prime} B F^{\prime}=90^{\circ}$，且 $AF^\prime、BP、CD^\prime$ 三线共点，不妨设 $F^\prime$ 在线段 $PF$ 内，则 $D^\prime$ 在线段 $AD$ 内，于是 $\dfrac{P F^{\prime}}{F^{\prime} C}<\dfrac{P F}{F C}, \dfrac{A D^{\prime}}{P D^\prime}<\dfrac{A D}{P D}$，所以 $\dfrac{P F^{\prime}}{F^{\prime} C} \cdot \dfrac{C B}{B A} \cdot \dfrac{A D^{\prime}}{D^{\prime} P}<\dfrac{P F}{F C} \cdot \dfrac{C B}{B A} \cdot \dfrac{A D}{P D}=1$．这与 $A F^{\prime}, B P, C D^{\prime}$ 三线共点矛盾．
所以，$BF$ 是 $\angle PBC$ 的内角平分线．
（2）不妨设圆 $O$ 的半径为 $1$，$\angle P C B=\alpha$，由（1）知，$\angle P B E=\angle E B C=30^{\circ}$，$E$ 是 $\overparen{PC}$ 的中点．因为 $\angle M P E=\angle P B E=30^{\circ}, \angle C P E=\angle C B E=30^{\circ}$，所以由 $PD=PE$ 知，$\angle P D E=\angle P E D=15^{\circ}$，$P E=2 \cdot 1 \cdot \sin 30^{\circ}=1, D E=2 \cos 15^{\circ}$．
又 $B E=2 \sin \angle E C B=2 \sin \left(\alpha+30^{\circ}\right), \angle B E D=\angle B E P-15^{\circ}=\alpha-15^{\circ}$，所以，在直角三角形 $BDE$ 中，有
$\cos \left(\alpha-15^{\circ}\right)=\dfrac{B E}{D E}=\dfrac{2 \sin \left(\alpha+30^{\circ}\right)}{2 \cos 15^{\circ}}$
$\cos \left(\alpha-15^{\circ}\right) \cos 15^{\circ}=\sin \left(\alpha+30^{\circ}\right)$
$\cos \alpha+\cos \left(\alpha-30^{\circ}\right)=2 \sin \left(\alpha+30^{\circ}\right)$
$\cos \alpha+\cos \alpha \cos 30^{\circ}+\sin \alpha \sin 30^{\circ}=\sqrt{3} \sin \alpha+\cos \alpha$
$1+\dfrac{\sqrt{3}}{2}+\dfrac{1}{2} \tan \alpha=\sqrt{3} \tan \alpha+1$
所以 $\tan \alpha=\dfrac{6+\sqrt{3}}{11}$．
答案
解析
备注
