如图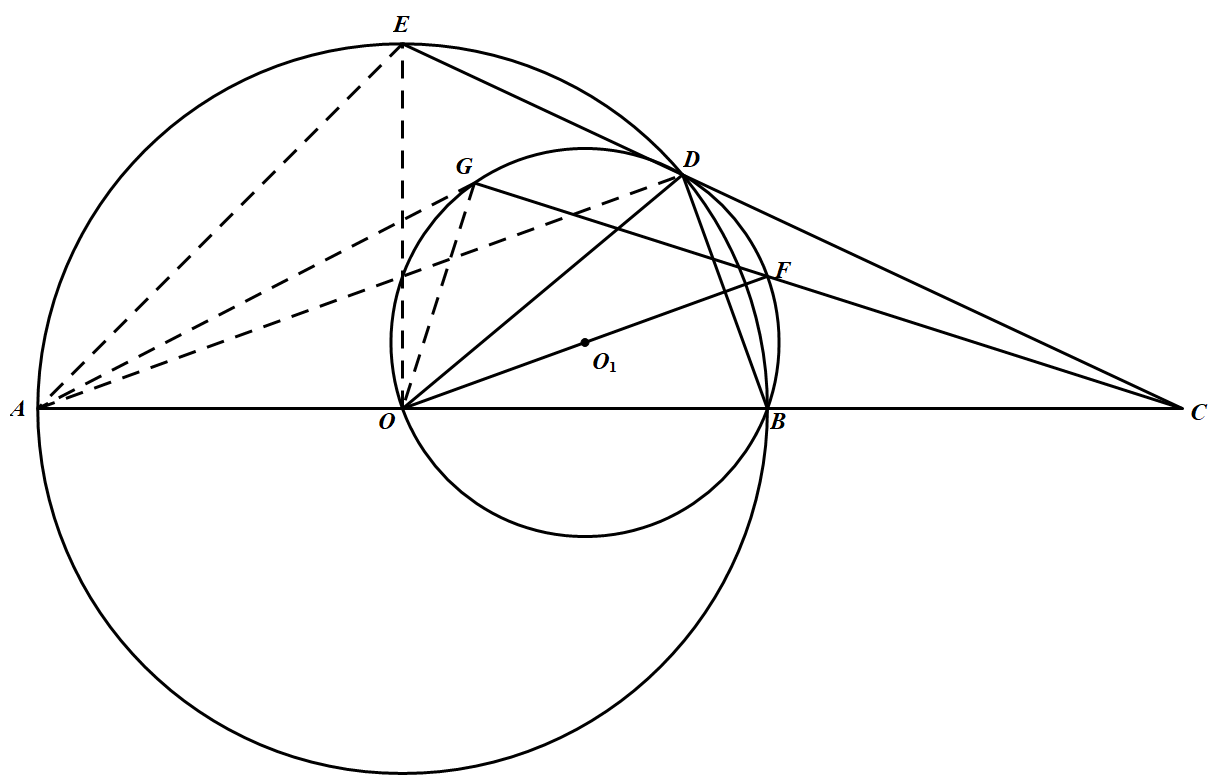
$AB$ 是圆 $O$ 的直径，$C$ 为 $AB$ 延长线上的一点，过点 $C$ 作圆 $O$ 的割线，与圆 $O$ 交于 $D、E$ 两点，$OF$ 是 $\triangle BOD$ 的外接圆 $O_1$ 的直径，连接 $ CF$ 并延长交圆 $O_1$ 于点 $G$．求证：$O、A、E,G$ 四点共圆．
$AB$ 是圆 $O$ 的直径，$C$ 为 $AB$ 延长线上的一点，过点 $C$ 作圆 $O$ 的割线，与圆 $O$ 交于 $D、E$ 两点，$OF$ 是 $\triangle BOD$ 的外接圆 $O_1$ 的直径，连接 $ CF$ 并延长交圆 $O_1$ 于点 $G$．求证：$O、A、E,G$ 四点共圆．【难度】
【出处】
2006年中国西部数学奥林匹克试题
【标注】
【答案】
略
【解析】
连接 $AD、DG、GA、GO、EA、EO$．因为 $OF$ 是等腰 $\triangle DOB$ 的外接圆的直径，所以 $OF$ 平分 $\angle DOB$，即 $\angle DOB =2\angle DOF$．又 $\angle D A B=\dfrac{1}{2} \angle D O B$，所以 $\angle D A B=\angle D O F$．
又 $\angle DGF= \angle DOF$，所以 $\angle DAB=\angle DGF$，所以，$G,A,C,D$ 四点共圆．
所以 $\angle A G C=\angle A D C$ ①
而 $\angle A G C=\angle A G O+\angle O G F=\angle A G O+\dfrac{\pi}{2}$ ②
$\angle \mathrm{ADC}=\angle A D B+\angle B D C=\dfrac{\pi}{2}+\angle B D C$ ③
结合 ①、②、③ 得 $\angle A G O=\angle B D C$ ④
因为 $B、D、E、A $ 四点共圆，所以 $\angle B D C=\angle E A O$ ⑤
又 $OA=OE$，所以 $\angle E A O=\angle A E O$ ⑥
由 ④、⑤、⑥ 得 $\angle A G O=\angle A E O$．
所以，$O,A,E,G$ 四点共圆．
又 $\angle DGF= \angle DOF$，所以 $\angle DAB=\angle DGF$，所以，$G,A,C,D$ 四点共圆．
所以 $\angle A G C=\angle A D C$ ①
而 $\angle A G C=\angle A G O+\angle O G F=\angle A G O+\dfrac{\pi}{2}$ ②
$\angle \mathrm{ADC}=\angle A D B+\angle B D C=\dfrac{\pi}{2}+\angle B D C$ ③
结合 ①、②、③ 得 $\angle A G O=\angle B D C$ ④
因为 $B、D、E、A $ 四点共圆，所以 $\angle B D C=\angle E A O$ ⑤
又 $OA=OE$，所以 $\angle E A O=\angle A E O$ ⑥
由 ④、⑤、⑥ 得 $\angle A G O=\angle A E O$．
所以，$O,A,E,G$ 四点共圆．
答案
解析
备注
