如图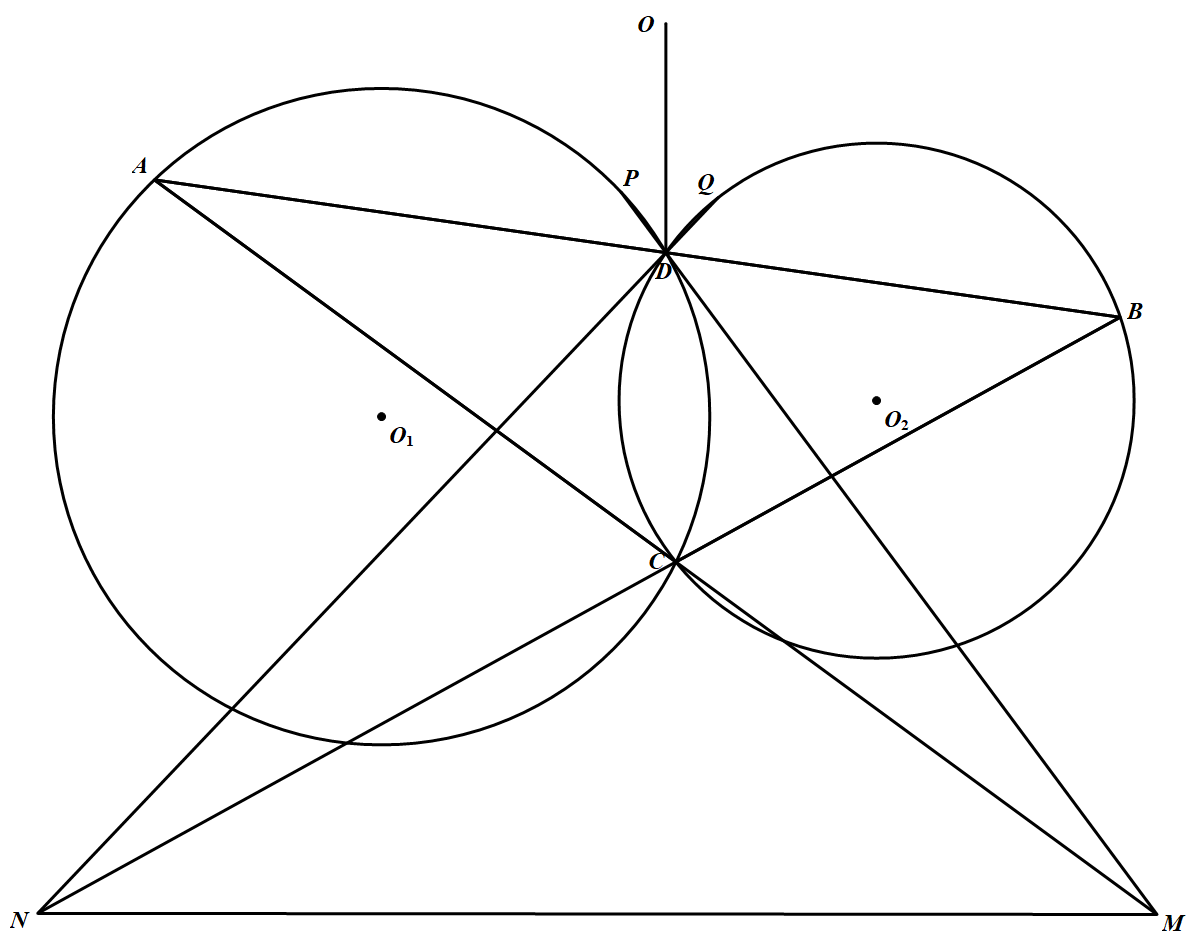
$\odot O_1$ 与 $\odot O_2$ 相交于点 $C、D$，过点 $D$ 的一条直线分别与 $\odot O_1,\odot O_2$ 相交于点 $A、B$，点 $P$ 在 $\odot O_1$ 的弧 $AD$ 上，$PD$ 与线段 $AC$ 的延长线交于点 $M$，点 $Q$ 在 $\odot O_2$ 的弧 $BD$ 上，$QD$ 与线段 $BC$ 的延长线交于点 $N$．$O$ 是 $\triangle ABC$ 的外心．求证：$OD\bot MN$ 的充要条件为 $P,Q,M,N$ 四点共圆．
$\odot O_1$ 与 $\odot O_2$ 相交于点 $C、D$，过点 $D$ 的一条直线分别与 $\odot O_1,\odot O_2$ 相交于点 $A、B$，点 $P$ 在 $\odot O_1$ 的弧 $AD$ 上，$PD$ 与线段 $AC$ 的延长线交于点 $M$，点 $Q$ 在 $\odot O_2$ 的弧 $BD$ 上，$QD$ 与线段 $BC$ 的延长线交于点 $N$．$O$ 是 $\triangle ABC$ 的外心．求证：$OD\bot MN$ 的充要条件为 $P,Q,M,N$ 四点共圆．【难度】
【出处】
2007年中国西部数学奥林匹克试题
【标注】
【答案】
略
【解析】
设三角形 $ABC$ 的外接圆 $O$ 的半径为 $R$，从 $N$ 到圆 $O$ 的切线为 $NX$，则 $N O^{2}=N X^{2}+R^{2}=N C \cdot N B+R^{2}$ ①
同理 $M O^{2}=M C \cdot M A+R^{2}$ ②
又因为 $A、C、D、P$ 四点共圆，所以 $M C \cdot M A=M D \cdot M P$ ③
同理由 $Q、D、C、B$ 四点共圆，得 $N C \cdot N B=N D \cdot N Q$ ④
由 ①、②、③、④ 得
$\begin{aligned} N O^{2}-M O^{2} &=N D \cdot N Q-M D \cdot M P =N D(N D+D Q)-M D(M D+D P) =N D^{2}-M D^{2}+(N D \cdot D Q-M D \cdot D P) \end{aligned}$
所以，$\begin{aligned} O D \perp M N & \Leftrightarrow N O^{2}-M O^{2}=N D^{2}-M D^{2} \Leftrightarrow N D \cdot D Q=M D \cdot D P \end{aligned}\Leftrightarrow P, Q, M, N$ 四点共圆
同理 $M O^{2}=M C \cdot M A+R^{2}$ ②
又因为 $A、C、D、P$ 四点共圆，所以 $M C \cdot M A=M D \cdot M P$ ③
同理由 $Q、D、C、B$ 四点共圆，得 $N C \cdot N B=N D \cdot N Q$ ④
由 ①、②、③、④ 得
$\begin{aligned} N O^{2}-M O^{2} &=N D \cdot N Q-M D \cdot M P =N D(N D+D Q)-M D(M D+D P) =N D^{2}-M D^{2}+(N D \cdot D Q-M D \cdot D P) \end{aligned}$
所以，$\begin{aligned} O D \perp M N & \Leftrightarrow N O^{2}-M O^{2}=N D^{2}-M D^{2} \Leftrightarrow N D \cdot D Q=M D \cdot D P \end{aligned}\Leftrightarrow P, Q, M, N$ 四点共圆
答案
解析
备注
