将 $n$ 个白子与 $n$ 个黑子任意地放在一个圆周上．从某个白子起，按顺时针方向依次将白子标以 $1,2, \cdots, n$．再从某个黑子起，按逆时针方向依次将黑子标以 $1,2, \cdots, n$．证明：存在 连续 $n$ 个棋子（不计黑白），它们的标号所成的集合为 $\{1,2, \cdots, n\}$．
【难度】
【出处】
2007年中国西部数学奥林匹克试题
【标注】
【答案】
略
【解析】
取定标号相同的黑白棋子各一个，使得该对点所决定的劣弧中其他点（不含端点，不计黑白）的个数最少．不妨假设该标号为 $1$．
在上述所取的开劣弧中，只有一种颜色的棋子．
事实上，若两个 $1$ 之间有两种颜色的棋 子，则白 $n$ 和黑 $n$ 都在其中，如图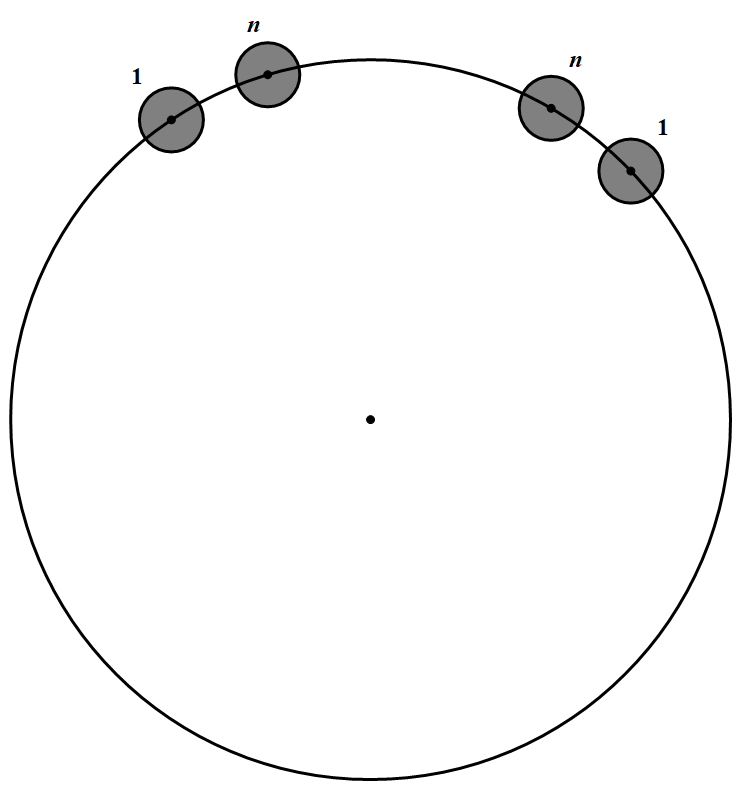
于是两个标号为 $n$ 的劣弧之间的点比两个标号为 $1$ 的更少，矛盾！
如果开劣弧中全是白子，有如下两种情形：
（1）开劣弧中的白子是 $2,\cdots, k$，如图所示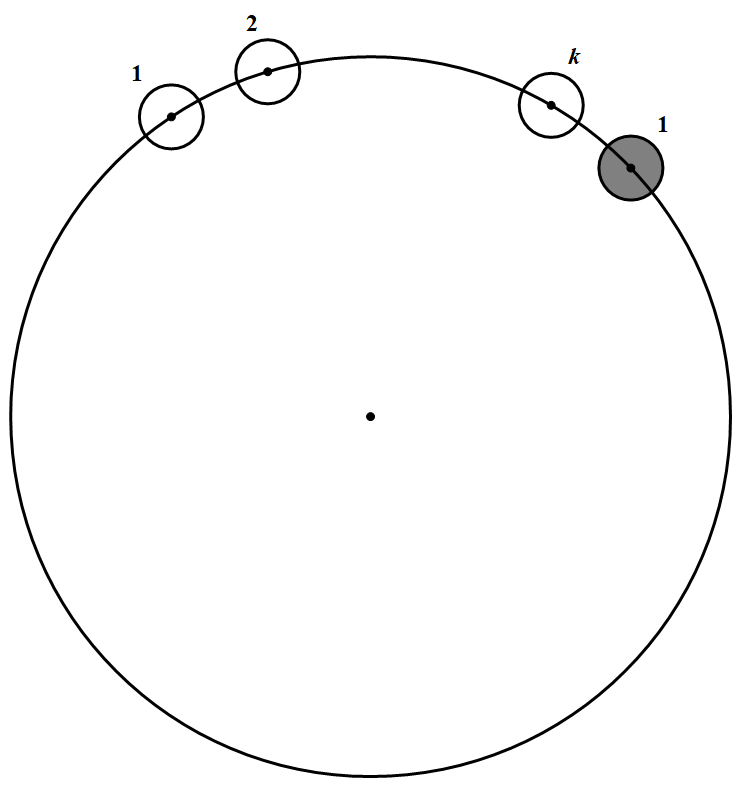
则从标号为 $1$ 的白子起，按逆时针方向连续 $n$ 个棋子的标号所成的集合为 $\{1,2, \cdots, n\}$
（2）开劣弧中的白子是 $k,k+ 1,\cdots,n$，如图所示
则从标号为 $1$ 的白子起，按顺时针方向连续 $n$ 个棋子的标号所成的集合为 $\{1,2, \cdots, n\}$
如果开劣弧中全是黑子，或者开劣弧中没有棋子，类似可得．
在上述所取的开劣弧中，只有一种颜色的棋子．
事实上，若两个 $1$ 之间有两种颜色的棋 子，则白 $n$ 和黑 $n$ 都在其中，如图
于是两个标号为 $n$ 的劣弧之间的点比两个标号为 $1$ 的更少，矛盾！如果开劣弧中全是白子，有如下两种情形：
（1）开劣弧中的白子是 $2,\cdots, k$，如图所示
则从标号为 $1$ 的白子起，按逆时针方向连续 $n$ 个棋子的标号所成的集合为 $\{1,2, \cdots, n\}$（2）开劣弧中的白子是 $k,k+ 1,\cdots,n$，如图所示
则从标号为 $1$ 的白子起，按顺时针方向连续 $n$ 个棋子的标号所成的集合为 $\{1,2, \cdots, n\}$如果开劣弧中全是黑子，或者开劣弧中没有棋子，类似可得．
答案
解析
备注
