如图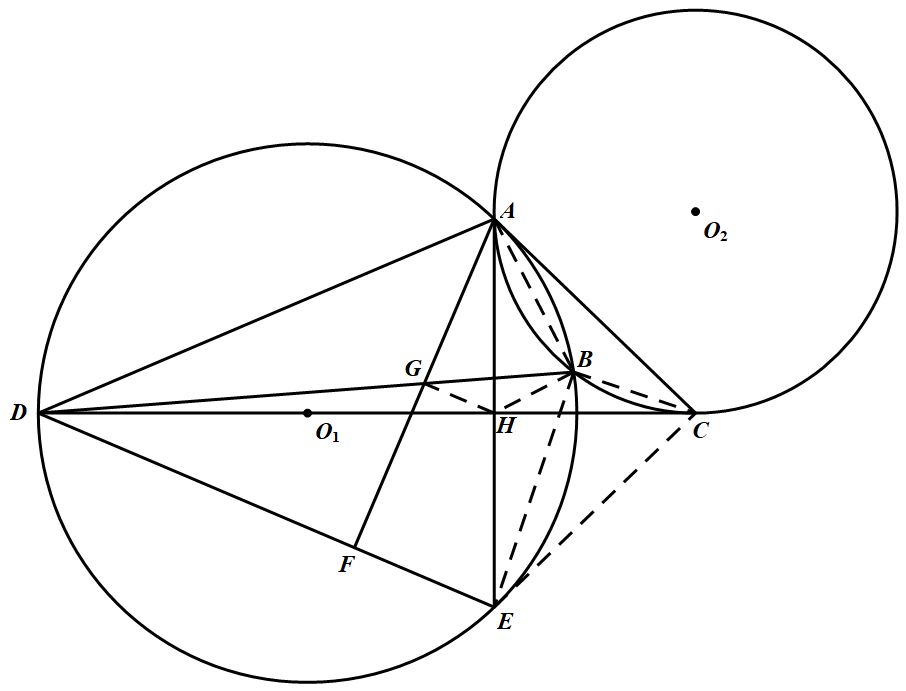
圆 $O_1$ 与圆 $O_2$ 交于 $A、B$ 两点．过点 $O_1$ 的直线 $DC$ 交圆 $O_1$ 于D且切圆 $O_2$ 于 $C$，$CA$ 切圆 $O_1$ 于 $A$，圆 $O_1$ 的弦 $AE$ 与直线 $DC$ 垂直．过 $A$ 作 $AF$ 垂直于 $DE$，$F$ 为垂足．求证：$BD$ 平分线段 $AF$．
圆 $O_1$ 与圆 $O_2$ 交于 $A、B$ 两点．过点 $O_1$ 的直线 $DC$ 交圆 $O_1$ 于D且切圆 $O_2$ 于 $C$，$CA$ 切圆 $O_1$ 于 $A$，圆 $O_1$ 的弦 $AE$ 与直线 $DC$ 垂直．过 $A$ 作 $AF$ 垂直于 $DE$，$F$ 为垂足．求证：$BD$ 平分线段 $AF$．【难度】
【出处】
2005年中国西部数学奥林匹克试题
【标注】
【答案】
略
【解析】
设 $AE$ 交 $DC$ 于 $H$，$AF$ 交 $BD$ 于 $G$，连接 $AB,BC,B H, B E, C E, G H$，由对称性知 $C E$ 边也是圆 $O_1$ 的切线，$H$ 为 $AE$ 的中点．因为 $\angle H C B=\angle B A C, \angle B A C=\angle B E H$，所以 $\angle H C B=\angle H E B$，$H、B、C、E$ 四点共圆，于是 $\angle B H C=\angle B E C$．
又 $\angle B E C=\angle B D E$，所以 $\angle B H C=\angle B D E$．①
而 $A F \perp D E \Rightarrow \angle A G B=\dfrac{\pi}{2}-\angle B D E$ ②
$A E \perp D C \Rightarrow \angle A H B=\dfrac{\pi}{2}-\angle B H C$ ③
由 ①②③ 得：$\angle A G B=\angle A H B$，所以 $A、G、H、B$ 四点共圆，进而 $\angle A H G=\angle A B G=\angle A E D$，于是 $G H \parallel D E$．
而 $H$ 为 $AE$ 的中点，故 $ G$ 为 $AF$ 的中点．
又 $\angle B E C=\angle B D E$，所以 $\angle B H C=\angle B D E$．①
而 $A F \perp D E \Rightarrow \angle A G B=\dfrac{\pi}{2}-\angle B D E$ ②
$A E \perp D C \Rightarrow \angle A H B=\dfrac{\pi}{2}-\angle B H C$ ③
由 ①②③ 得：$\angle A G B=\angle A H B$，所以 $A、G、H、B$ 四点共圆，进而 $\angle A H G=\angle A B G=\angle A E D$，于是 $G H \parallel D E$．
而 $H$ 为 $AE$ 的中点，故 $ G$ 为 $AF$ 的中点．
答案
解析
备注
