在等腰直角 $\triangle ABC$ 中，$CA=CB= 1$，点 $P$ 是 $\triangle ABC$ 边界上任意一点，求 $P A \cdot P B \cdot P C$ 的最大值．
【难度】
【出处】
2005年中国西部数学奥林匹克试题
【标注】
【答案】
略
【解析】
首先证明取到最大值只有当 $P\in AB$ 时，才可能取到．
（1）当 $ P\in AC$ 时，有
$P A \cdot P C \leqslant \dfrac{1}{4}, P B \leqslant \sqrt{2}$，故 $P A \cdot P B \cdot P C \leqslant \dfrac{\sqrt{2}}{4}$，其中等号不成立（因为两个等号不可能同时成立），即 $P A \cdot P B \cdot P C<\dfrac{\sqrt{2}}{4}$．
（2）当 $P\in AB$ 时，设 $AP=x\in [0, \sqrt{2}］$，则
$\begin{aligned} f(x) &=P A^{2} \cdot P B^{2} \cdot P C^{2} =x^{2}(\sqrt{2}-x)^{2}\left(1+x^{2}-\sqrt{2} x\right) \end{aligned}$．
令 $t=x(\sqrt{2}-x)$，则 $t \in\left[0, \dfrac{1}{2}\right], f(x)=g(t)=t^{2}(1-t)$．
注意到 $g^{\prime}(t)=2 t-3 t^{2}=t(2-3 t)$，故 $g(t)$ 在 $\left[0, \dfrac{2}{3}\right]$ 上递增，所以f $f(x) \leqslant g\left(\dfrac{1}{2}\right)=\dfrac{1}{8}$，故 $P A \cdot P B \cdot P C \leqslant \dfrac{1}{2 \sqrt{2}}=\dfrac{\sqrt{2}}{4}$．等号成立当且仅当 $t=\dfrac{1}{2}, x=\dfrac{\sqrt{2}}{2}$，即 $P$ 为 $AB$ 的中点时取等号．
证法二
（1）当 $P$ 在线段 $AB$ 上时，过 $C$ 作 $CD\bot AB$ 于 $D$．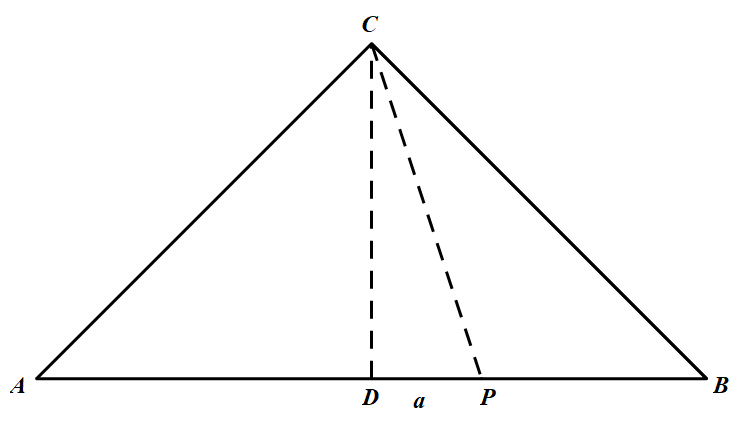
设 $PD=a$，则 $P A \cdot P B=\dfrac{1}{2}-a^{2}, P C=\sqrt{\dfrac{1}{2}+a^{2}}$，所以
$\begin{aligned} P A \cdot P B \cdot P C &=\left(\frac{1}{2}-a^{2}\right) \cdot \sqrt{\frac{1}{2}+a^{2}} \\ & \leqslant \sqrt{\frac{1}{2}} \cdot \sqrt{\frac{1}{2}-a^{2}} \cdot \sqrt{\frac{1}{2}+a^{2}} \\ & \leqslant \frac{\sqrt{2}}{2} \cdot \sqrt{\frac{1}{4}} \\ &=\frac{\sqrt{2}}{4} \end{aligned}$
当 $a=0$ 时，上式取等号．
（2）当 $P$ 在直角边上时，不妨设 $P$ 在 $ BC$ 上，记 $PC=b$，则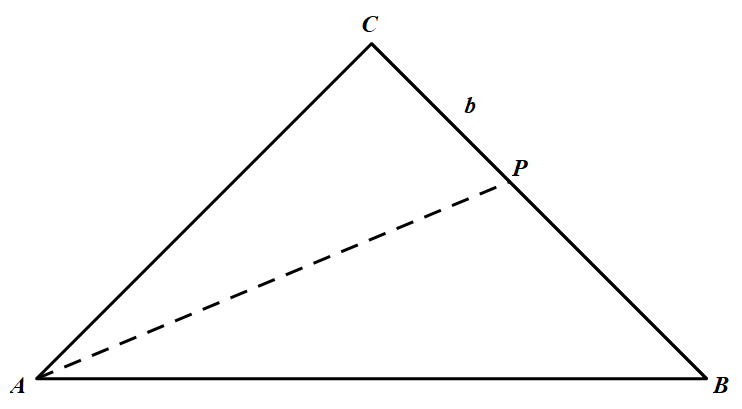
$\begin{aligned} P A \cdot P B \cdot P C &=b(1-b) \sqrt{1+b^{2}} \\ & \leqslant\left(\frac{b+1-b}{2}\right)^{2} \sqrt{1+b^{2}} \\ &=\frac{1}{4} \sqrt{1+b^{2}} \leqslant \frac{1}{4} \sqrt{1+1^{2}} \\ &=\frac{\sqrt{2}}{4} \end{aligned}$
上式显然不能取等号．
因此 $P A \cdot P B \cdot P C$ 的最大值为 $\dfrac{\sqrt{2}}{4}$．当 $P$ 在 $AB$ 中点时取等号．
（1）当 $ P\in AC$ 时，有
$P A \cdot P C \leqslant \dfrac{1}{4}, P B \leqslant \sqrt{2}$，故 $P A \cdot P B \cdot P C \leqslant \dfrac{\sqrt{2}}{4}$，其中等号不成立（因为两个等号不可能同时成立），即 $P A \cdot P B \cdot P C<\dfrac{\sqrt{2}}{4}$．（2）当 $P\in AB$ 时，设 $AP=x\in [0, \sqrt{2}］$，则
$\begin{aligned} f(x) &=P A^{2} \cdot P B^{2} \cdot P C^{2} =x^{2}(\sqrt{2}-x)^{2}\left(1+x^{2}-\sqrt{2} x\right) \end{aligned}$．令 $t=x(\sqrt{2}-x)$，则 $t \in\left[0, \dfrac{1}{2}\right], f(x)=g(t)=t^{2}(1-t)$．
注意到 $g^{\prime}(t)=2 t-3 t^{2}=t(2-3 t)$，故 $g(t)$ 在 $\left[0, \dfrac{2}{3}\right]$ 上递增，所以f $f(x) \leqslant g\left(\dfrac{1}{2}\right)=\dfrac{1}{8}$，故 $P A \cdot P B \cdot P C \leqslant \dfrac{1}{2 \sqrt{2}}=\dfrac{\sqrt{2}}{4}$．等号成立当且仅当 $t=\dfrac{1}{2}, x=\dfrac{\sqrt{2}}{2}$，即 $P$ 为 $AB$ 的中点时取等号．
证法二
（1）当 $P$ 在线段 $AB$ 上时，过 $C$ 作 $CD\bot AB$ 于 $D$．
设 $PD=a$，则 $P A \cdot P B=\dfrac{1}{2}-a^{2}, P C=\sqrt{\dfrac{1}{2}+a^{2}}$，所以$\begin{aligned} P A \cdot P B \cdot P C &=\left(\frac{1}{2}-a^{2}\right) \cdot \sqrt{\frac{1}{2}+a^{2}} \\ & \leqslant \sqrt{\frac{1}{2}} \cdot \sqrt{\frac{1}{2}-a^{2}} \cdot \sqrt{\frac{1}{2}+a^{2}} \\ & \leqslant \frac{\sqrt{2}}{2} \cdot \sqrt{\frac{1}{4}} \\ &=\frac{\sqrt{2}}{4} \end{aligned}$
当 $a=0$ 时，上式取等号．
（2）当 $P$ 在直角边上时，不妨设 $P$ 在 $ BC$ 上，记 $PC=b$，则
$\begin{aligned} P A \cdot P B \cdot P C &=b(1-b) \sqrt{1+b^{2}} \\ & \leqslant\left(\frac{b+1-b}{2}\right)^{2} \sqrt{1+b^{2}} \\ &=\frac{1}{4} \sqrt{1+b^{2}} \leqslant \frac{1}{4} \sqrt{1+1^{2}} \\ &=\frac{\sqrt{2}}{4} \end{aligned}$上式显然不能取等号．
因此 $P A \cdot P B \cdot P C$ 的最大值为 $\dfrac{\sqrt{2}}{4}$．当 $P$ 在 $AB$ 中点时取等号．
答案
解析
备注
