设 $n$ 个新生中，任意 $3$ 个人中有 $2$ 个人互相认识，任意 $ 4$ 个人中有 $2$ 个人互不认识．试求 $n$ 的最大值．
【难度】
【出处】
2005年中国西部数学奥林匹克试题
【标注】
【答案】
略
【解析】
所求 $n$ 的最大值为 $8$．
当 $n=8$ 时，如图所示的例子满足要求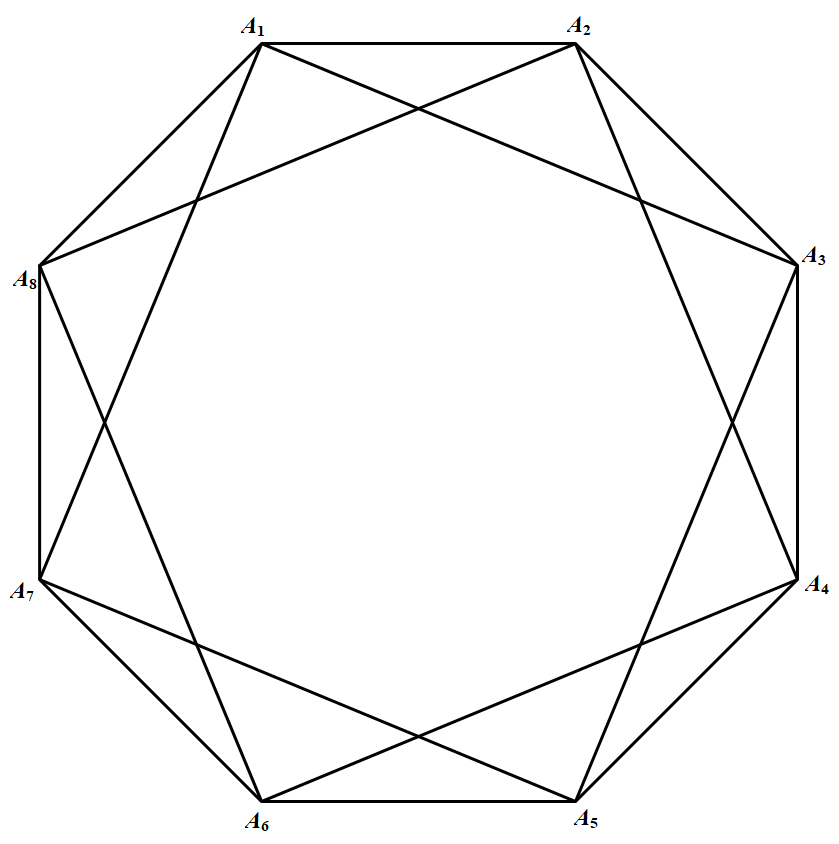
其中 $A_{1}, A_{2}, \cdots, A_{8}$ 表示 $8$ 个学生，$A_i$ 与 $A_j$ 连线表示 $A_i$ 与 $A_j$ 认识，否则不认识．
下设 $n$ 个学生满足题设要求，我们来证明 $n\leqslant 8$．为此，我们先来证明如下两种情况不可能出现：
（1）若某人 $A$ 至少认识 $6$ 个人，设为 $B_{1}, \cdots, B_{6}$ 由Ramsey定理，这 $6$ 个人中存在 $3$ 个互不相识（这与已知任 $3$ 个人中有 $2$ 个 相识矛盾）；或存在 $3$ 个人互相认识，这时 $A$ 与这 $3$ 个人共 $4$ 人两两互相认识，亦与已知矛盾．
（2）若某人 $A$ 至多认识 $n-5$ 个人，则剩下至少 $4$ 个人均与 $A$ 不相识，从而这 $4$ 个人两两相识，矛盾．
其次，当 $n\geqslant 10$ 时，（1）与（2）必有一种情况出现，故此时 $n$ 不满足要求；当 $n=9$ 时，要使（1）与（2）均不出现，则此时每个人恰好 认识其他 $5$ 个人，于是这时 $9$ 个人产生的朋友对（相互认识的对子）的数目为 $\frac{9 \times 5}{2} \notin \mathbf{N}^{*}$，矛盾！
由上可知，满足要求的只有 $n\leqslant 8$．综上，所求 $n$ 的最大值为 $8$．
当 $n=8$ 时，如图所示的例子满足要求
其中 $A_{1}, A_{2}, \cdots, A_{8}$ 表示 $8$ 个学生，$A_i$ 与 $A_j$ 连线表示 $A_i$ 与 $A_j$ 认识，否则不认识．下设 $n$ 个学生满足题设要求，我们来证明 $n\leqslant 8$．为此，我们先来证明如下两种情况不可能出现：
（1）若某人 $A$ 至少认识 $6$ 个人，设为 $B_{1}, \cdots, B_{6}$ 由Ramsey定理，这 $6$ 个人中存在 $3$ 个互不相识（这与已知任 $3$ 个人中有 $2$ 个 相识矛盾）；或存在 $3$ 个人互相认识，这时 $A$ 与这 $3$ 个人共 $4$ 人两两互相认识，亦与已知矛盾．
（2）若某人 $A$ 至多认识 $n-5$ 个人，则剩下至少 $4$ 个人均与 $A$ 不相识，从而这 $4$ 个人两两相识，矛盾．
其次，当 $n\geqslant 10$ 时，（1）与（2）必有一种情况出现，故此时 $n$ 不满足要求；当 $n=9$ 时，要使（1）与（2）均不出现，则此时每个人恰好 认识其他 $5$ 个人，于是这时 $9$ 个人产生的朋友对（相互认识的对子）的数目为 $\frac{9 \times 5}{2} \notin \mathbf{N}^{*}$，矛盾！
由上可知，满足要求的只有 $n\leqslant 8$．综上，所求 $n$ 的最大值为 $8$．
答案
解析
备注
