$ABCD$ 为一凸四边形，$I_1,I_2$ 分别为 $\triangle A B C, \triangle D B C$ 内心，过点 $I_1,I_2$ 的直线分别交 $AB、DC$ 于点 $E、F$，分别延长 $ AB$ 和 $DC$，它们相交于点 $P$，且 $PE=PF$，求证：$A、B、C、P$ 四点共圆．
【难度】
【出处】
2004年中国西部数学奥林匹克试题
【标注】
【答案】
略
【解析】
如图，连结 $I_{1} B, I_{1} C, I_{2} B, I_{2} C$．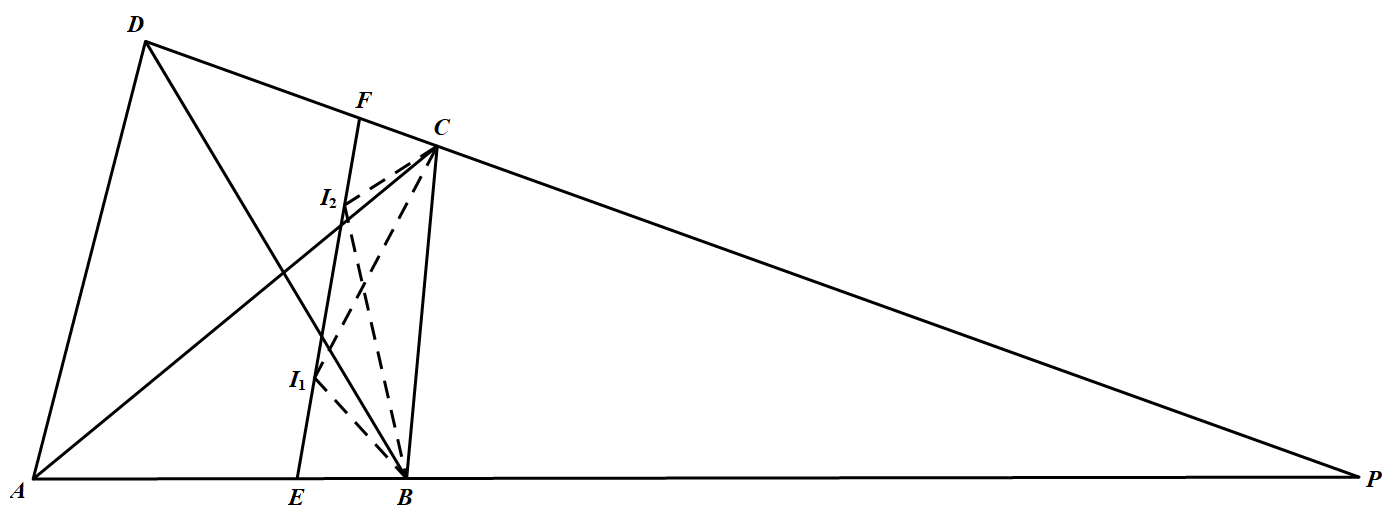
因为 $P E=P F$，所以 $\angle P E F=\angle P F E$．
而 $\angle P E F=\angle I_{2} I_{1} B-\angle E B I_{1}=\angle I_{2} I_{1} B-\angle I_{1} B C$
$\angle P F E=\angle I_{1} I_{2} C-\angle F C I_{2}=\angle I_{1} I_{2} C-\angle I_{2} C B$
所以 $\angle I_{2} I_{1} B-\angle I_{1} B C=\angle I_{1} I_{2} C-\angle I_{2} C B$，
即 $\angle I_{2} I_{1} B+\angle I_{2} C B=\angle I_{1} I_{2} C+\angle I_{1} B C$．
又 $\angle I_{2} I_{1} B+\angle I_{2} C B+\angle I_{1} I_{2} C+\angle I_{1} B C=2 \pi$，
所以 $\angle I_{2} I_{1} B+\angle I_{2} C B=\pi$，
所以 $I_{1}, I_{2}, C, B$ 四点共圆．
因此 $\angle B I_{1} C=\angle B I_{2} C$，所以
$\begin{aligned} \angle I_{1} B C+\angle I_{1} C B &=\angle I_{2} B C+\angle I_{2} C B \\ \angle A B C+\angle A C B &=\angle D B C+\angle D C B \end{aligned}$
所以 $\angle B A C=\angle B D C$，故四点共圆．
因为 $P E=P F$，所以 $\angle P E F=\angle P F E$．而 $\angle P E F=\angle I_{2} I_{1} B-\angle E B I_{1}=\angle I_{2} I_{1} B-\angle I_{1} B C$
$\angle P F E=\angle I_{1} I_{2} C-\angle F C I_{2}=\angle I_{1} I_{2} C-\angle I_{2} C B$
所以 $\angle I_{2} I_{1} B-\angle I_{1} B C=\angle I_{1} I_{2} C-\angle I_{2} C B$，
即 $\angle I_{2} I_{1} B+\angle I_{2} C B=\angle I_{1} I_{2} C+\angle I_{1} B C$．
又 $\angle I_{2} I_{1} B+\angle I_{2} C B+\angle I_{1} I_{2} C+\angle I_{1} B C=2 \pi$，
所以 $\angle I_{2} I_{1} B+\angle I_{2} C B=\pi$，
所以 $I_{1}, I_{2}, C, B$ 四点共圆．
因此 $\angle B I_{1} C=\angle B I_{2} C$，所以
$\begin{aligned} \angle I_{1} B C+\angle I_{1} C B &=\angle I_{2} B C+\angle I_{2} C B \\ \angle A B C+\angle A C B &=\angle D B C+\angle D C B \end{aligned}$
所以 $\angle B A C=\angle B D C$，故四点共圆．
答案
解析
备注
