如图,在棱长为 $2$ 的正方体 $ABCD-A_1B_1C_1D_1$ 中,$A_1B_1$ 的中点是 $P$,过点 $A_1$ 作截面 $PBC_1$ 平行的截面,则该截面的面积为 \((\qquad)\) 

【难度】
【出处】
无
【标注】
【答案】
C
【解析】
截面是一个对角线分别为正方体体对角线和面对角线的菱形,则 $EF=2\sqrt{2}$,$A_1C=2\sqrt{3}$,
$EF⊥A_1C$,
则截面面积 $S=\dfrac{1}{2}EF\cdot A_1C=2\sqrt{6}$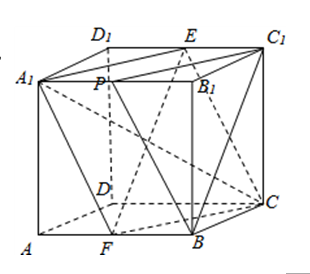
$EF⊥A_1C$,
则截面面积 $S=\dfrac{1}{2}EF\cdot A_1C=2\sqrt{6}$

题目
答案
解析
备注