证明：若凸四边形 $ABCD$ 内任意一点 $P$ 到四条边 $AB,BC,CD,DA$ 的距离之和为定值，则 $ABCD$ 是平行四边形．
【难度】
【出处】
2003年中国西部数学奥林匹克试题
【标注】
【答案】
略
【解析】
用记号 $d(P, l)$ 表示点 $P$ 到直线 $l$ 的距离．先证一个引理．
引理：设 $\angle S A T=a$ 是一个定角．$\angle SAT$ 内一动点 $P$ 到 $AS、AT$ 的距离之和为常数 $m$ 的轨迹是线段 $BC$．其中 $B、C$ 分别在 $AS、AT$ 上，且 $A B=A C=\dfrac{m}{\sin \alpha}$．且若点 $P$ 在 $\triangle ABC$ 内，则点 $P$ 到两边 $AS、AT$ 的距离之和 $<m$；若点 $P$ 在 $\triangle ABC$ 外，则点 $P$ 到两边 $AS、AT$ 的距离之和 $>m$．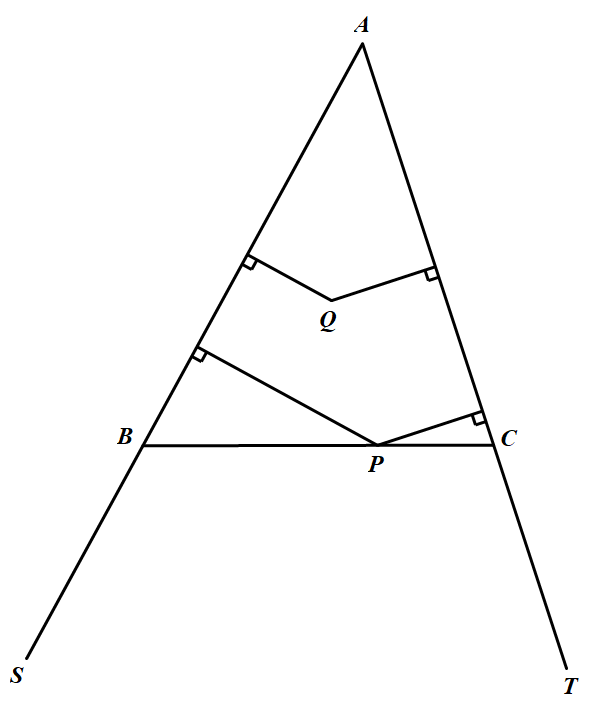
事实上，由 $S_{\triangle P A B}+S_{\triangle P A C}=S_{\triangle A B C}$，知 $d(P, A B)+d(P,A C )=m$．若点 $Q$ 在 $\triangle ABC$ 内，由 $S_{\triangle Q A B}+S_{\triangle Q A C}<S_{\triangle A B C}$，得 $d(Q, A B)+d(Q, A C)<m$；若 $Q$ 在 $\triangle ABC$ 外，由 $S_{\triangle Q 4 B}+S_{\triangle A C C}>S_{\triangle A B C}$，得 $d(Q, A B)+d(Q, A C)>m$．引理得证．
下面，我们分两种情况讨论．
（1）若四边形 $ABCD$ 的两组对边都不平行，不妨设 $BC$ 与 $AD$ 相交于点 $F$，$BA$ 与 $CD$ 相交于点 $E$．过点 $P$ 分别作线段 $l_1、l_2$ 使得 $l
_1$ 上的任意一点到 $AB、CD$ 的距离之和为常数，$l_2$ 上的任意一点到 $BC、AD$ 的距离之和为常数，如图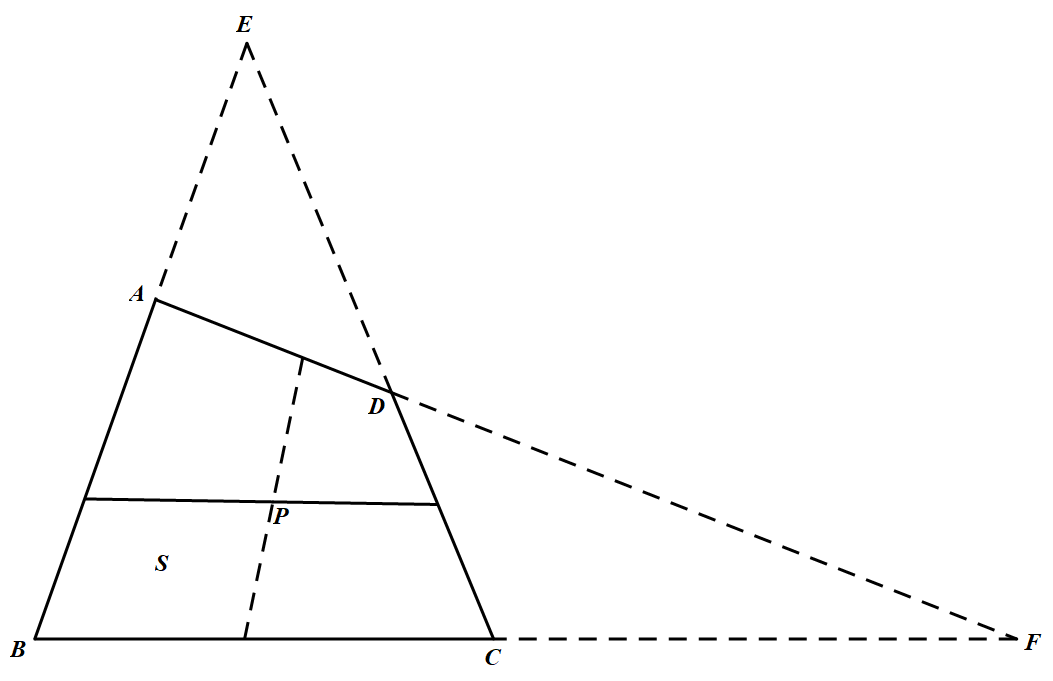
则对于区域 $S$ 内任意一点 $Q$，有
$\begin{aligned} &d(P, A B)+d(P, B C)+d(P, C D)+d(P, D A) \\& = d(Q, A B)+d(Q, B C)+d(Q, C D)+d(Q, D A) \\ &=[d(Q, A B)+d(Q, C D)]+[d(Q, B C)+d(Q, D A)]\\& >[d(P, A B)+d(P, C D)]+[d(P, B C)+d(P, D A)]\end{aligned}$
矛盾!
（2）四边形 $ABCD$ 是梯形时，同样可以推得矛盾．
于是，我们得到 $ABCD$ 是平行四边形．
引理：设 $\angle S A T=a$ 是一个定角．$\angle SAT$ 内一动点 $P$ 到 $AS、AT$ 的距离之和为常数 $m$ 的轨迹是线段 $BC$．其中 $B、C$ 分别在 $AS、AT$ 上，且 $A B=A C=\dfrac{m}{\sin \alpha}$．且若点 $P$ 在 $\triangle ABC$ 内，则点 $P$ 到两边 $AS、AT$ 的距离之和 $<m$；若点 $P$ 在 $\triangle ABC$ 外，则点 $P$ 到两边 $AS、AT$ 的距离之和 $>m$．
事实上，由 $S_{\triangle P A B}+S_{\triangle P A C}=S_{\triangle A B C}$，知 $d(P, A B)+d(P,A C )=m$．若点 $Q$ 在 $\triangle ABC$ 内，由 $S_{\triangle Q A B}+S_{\triangle Q A C}<S_{\triangle A B C}$，得 $d(Q, A B)+d(Q, A C)<m$；若 $Q$ 在 $\triangle ABC$ 外，由 $S_{\triangle Q 4 B}+S_{\triangle A C C}>S_{\triangle A B C}$，得 $d(Q, A B)+d(Q, A C)>m$．引理得证．下面，我们分两种情况讨论．
（1）若四边形 $ABCD$ 的两组对边都不平行，不妨设 $BC$ 与 $AD$ 相交于点 $F$，$BA$ 与 $CD$ 相交于点 $E$．过点 $P$ 分别作线段 $l_1、l_2$ 使得 $l
_1$ 上的任意一点到 $AB、CD$ 的距离之和为常数，$l_2$ 上的任意一点到 $BC、AD$ 的距离之和为常数，如图
则对于区域 $S$ 内任意一点 $Q$，有$\begin{aligned} &d(P, A B)+d(P, B C)+d(P, C D)+d(P, D A) \\& = d(Q, A B)+d(Q, B C)+d(Q, C D)+d(Q, D A) \\ &=[d(Q, A B)+d(Q, C D)]+[d(Q, B C)+d(Q, D A)]\\& >[d(P, A B)+d(P, C D)]+[d(P, B C)+d(P, D A)]\end{aligned}$
矛盾!
（2）四边形 $ABCD$ 是梯形时，同样可以推得矛盾．
于是，我们得到 $ABCD$ 是平行四边形．
答案
解析
备注
