凸多边形 $ABCD$ 有内切圆，该内切圆切边 $AB、BC、CD、DA$ 的切点分别为 $A_1、B_1、C_1、D_1$，连接 $A_1B_1、B_1C_1、C_1D_1、D_1A_1$，点 $E、F、G、H$ 分别为 $A_1B_1、B_1C_1、C_1D_1、D_1A_1$ 的中点．证明：四边形EFGH为矩形的充分必要条件是 $ A、B、C、D$ 四点共圆．
【难度】
【出处】
2003年中国西部数学奥林匹克试题
【标注】
【答案】
略
【解析】
如图所示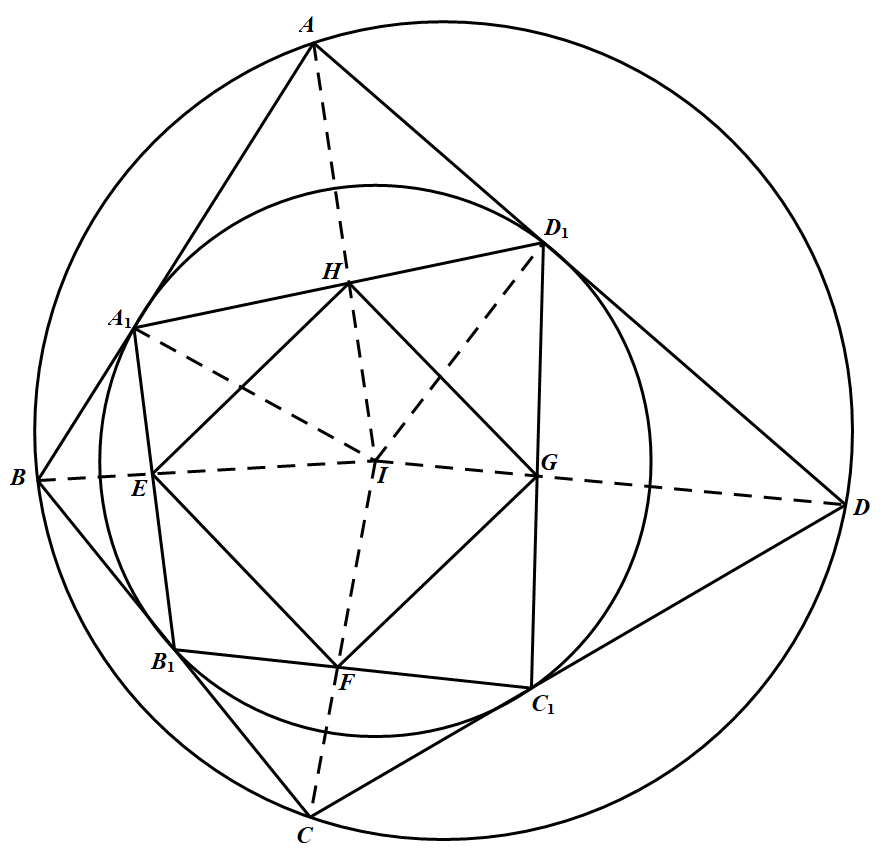
设 $I$ 为四边形 $ABCD$ 的内切圆的圆心．由于 $H$ 为 $D_1A_1$ 的中点，而 $AA_1$ 与 $AD_1$ 为过点 $A$ 所作的圆 $I$ 的切线，故 $H$ 在 $AI$ 上，且 $AI\bot A_1D_1$．又 $ID_{1} \bot A D_{1}$，故由射影定理可知 $IH\cdot I A=I D_{1}^{2}=r^{2}$，其中 $r$ 为内切圆半径．
同理可知，$E$ 在 $BI$ 上，且 $IE\cdot IB=r
^2$．于是，$IE\cdot IB = IH\cdot IA$，故点 $A,H,E,B$ 四点共圆，所以，$\angle E H I=\angle A B E$．
类似地，可证 $\angle I H G=\angle A D G, \angle I F E=\angle C B E, \angle I F G=\angle C D G$．将这四个式子相加得 $\angle E H G+\angle E F G=\angle A B C+\angle A D C$．
所以，$A,B,C,D$ 四点共圆的充要条件是 $E,F,G,H$ 四点共圆．而熟知一个四边形的各边中点围成的四边形是平行四边形，平行四边形为矩形的充要条件是该四边形的四个顶点共圆．命题获证．
设 $I$ 为四边形 $ABCD$ 的内切圆的圆心．由于 $H$ 为 $D_1A_1$ 的中点，而 $AA_1$ 与 $AD_1$ 为过点 $A$ 所作的圆 $I$ 的切线，故 $H$ 在 $AI$ 上，且 $AI\bot A_1D_1$．又 $ID_{1} \bot A D_{1}$，故由射影定理可知 $IH\cdot I A=I D_{1}^{2}=r^{2}$，其中 $r$ 为内切圆半径．同理可知，$E$ 在 $BI$ 上，且 $IE\cdot IB=r
^2$．于是，$IE\cdot IB = IH\cdot IA$，故点 $A,H,E,B$ 四点共圆，所以，$\angle E H I=\angle A B E$．
类似地，可证 $\angle I H G=\angle A D G, \angle I F E=\angle C B E, \angle I F G=\angle C D G$．将这四个式子相加得 $\angle E H G+\angle E F G=\angle A B C+\angle A D C$．
所以，$A,B,C,D$ 四点共圆的充要条件是 $E,F,G,H$ 四点共圆．而熟知一个四边形的各边中点围成的四边形是平行四边形，平行四边形为矩形的充要条件是该四边形的四个顶点共圆．命题获证．
答案
解析
备注
