设 $O$ 为锐角 $\triangle ABC$ 的 外心，$P$ 为 $\triangle AOB$ 内部一点，$P$ 在 $\triangle ABC$ 的 三边 $BC、CA、AB$ 上 的 射 影 分 别为 $D、E、F$．求 证：以 $F E、FD$ 为邻边的平行四边形位于 $ \triangle ABC$ 内．
【难度】
【出处】
2002年中国西部数学奥林匹克试题
【标注】
【答案】
略
【解析】
如图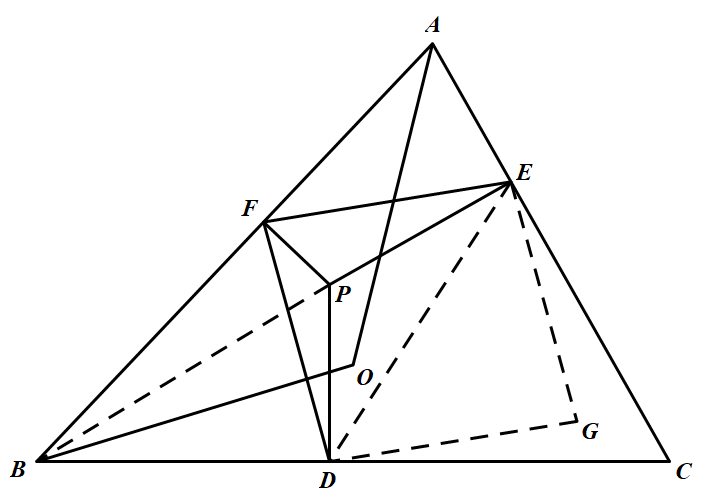
以 $FE,FD$ 为邻边作平行四边形 $EFDG$ 为证命题成立，
只须证明 $\angle F D E<\angle C E D$ ① 且 $\angle F E D<\angle E D C$ ②
注意到 ①，② 是对称的，故只须证明其中一式成立，另一式子可以完全类似地证明．
对于式 ①，由于 $\angle F D E=\angle F D P+\angle E D P$，而 $B, D, P, F$ 四点共圆，故 $\angle F D P=\angle F B P<\angle A B O=90^{\circ}-\dfrac{1}{2} \angle A O B=90^{\circ}-\angle C$
（这里用到 $P$ 在 $\triangle AOB$ 内部及 $O$ 为 $\triangle ABC$ 的外心）．
又 $C, E, P, D$ 四点共圆，故 $\angle P D E=\angle P C E,\angle C E D=\angle C P D=90^{\circ}-\angle P C D$
所以，$\angle F D E<\left(90^{\circ}-\angle C\right)+\angle P C E=90^{\circ}-\angle P C D=\angle C E D$
从而，式 ① 成立．命题获证．
以 $FE,FD$ 为邻边作平行四边形 $EFDG$ 为证命题成立，只须证明 $\angle F D E<\angle C E D$ ① 且 $\angle F E D<\angle E D C$ ②
注意到 ①，② 是对称的，故只须证明其中一式成立，另一式子可以完全类似地证明．
对于式 ①，由于 $\angle F D E=\angle F D P+\angle E D P$，而 $B, D, P, F$ 四点共圆，故 $\angle F D P=\angle F B P<\angle A B O=90^{\circ}-\dfrac{1}{2} \angle A O B=90^{\circ}-\angle C$
（这里用到 $P$ 在 $\triangle AOB$ 内部及 $O$ 为 $\triangle ABC$ 的外心）．
又 $C, E, P, D$ 四点共圆，故 $\angle P D E=\angle P C E,\angle C E D=\angle C P D=90^{\circ}-\angle P C D$
所以，$\angle F D E<\left(90^{\circ}-\angle C\right)+\angle P C E=90^{\circ}-\angle P C D=\angle C E D$
从而，式 ① 成立．命题获证．
答案
解析
备注
