如下图
四边形 $ABCD$ 为圆内接四边形，$I_1$ 为 $\triangle ABC$ 的内心，$I_2$ 为 $\triangle ABD$ 的内心，$J_1$ 为 $\triangle BCD$ 的点 $D$ 所对的旁心，$J_2$ 为 $\triangle ACD$ 的点 $C$ 所对的旁心．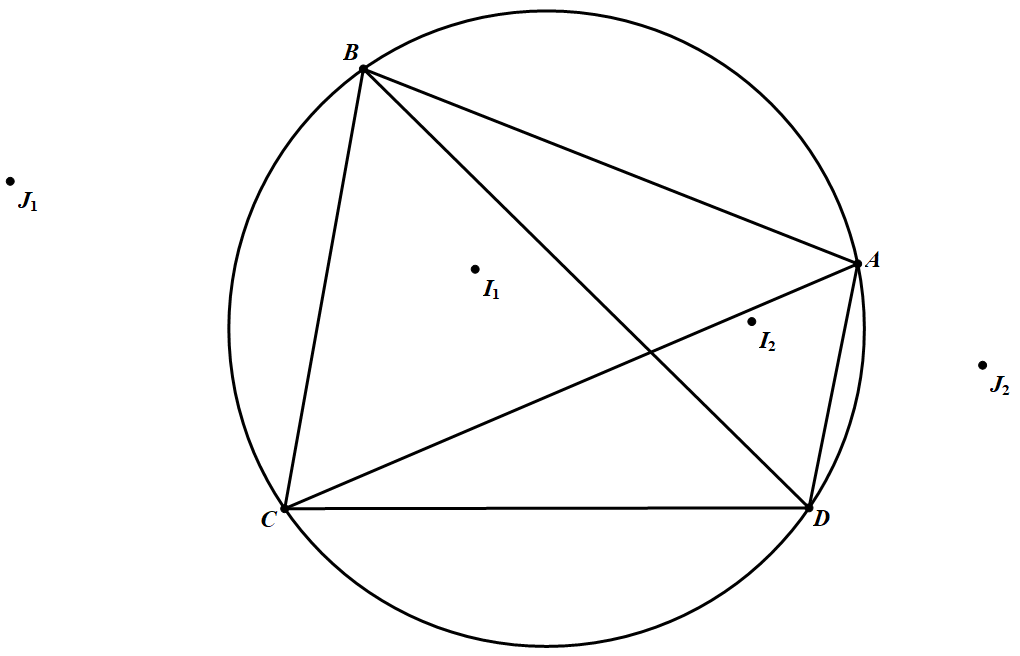
四边形 $ABCD$ 为圆内接四边形，$I_1$ 为 $\triangle ABC$ 的内心，$I_2$ 为 $\triangle ABD$ 的内心，$J_1$ 为 $\triangle BCD$ 的点 $D$ 所对的旁心，$J_2$ 为 $\triangle ACD$ 的点 $C$ 所对的旁心．
【难度】
【出处】
2019北京大学中学生数学奖个人能力挑战赛
【标注】
【答案】
略
【解析】
取 $\triangle BCD$ 的内心 $P$ 和 $\overparen BC$ 的中点 $Q$．则 $D,P,Q,J_1$ 四点共线．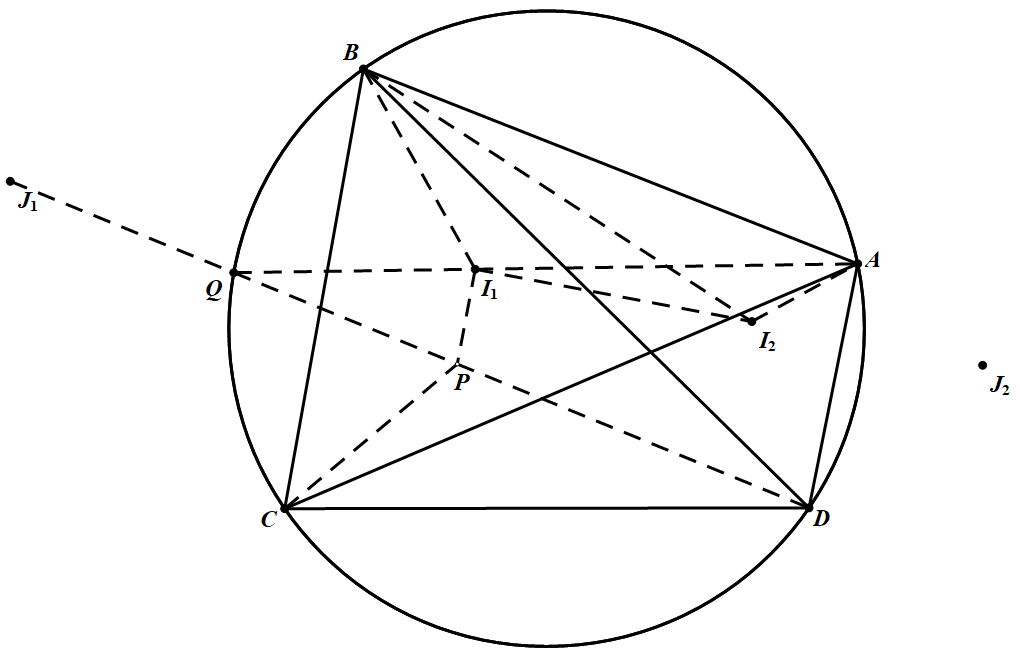
由鸡爪关系可得 $QP=QI_1=QJ_1$，从而 $\angle PI_1J_1=90^\circ$．
由 $\angle B I_{1} A=90^{\circ}+\frac{1}{2} \angle B C A=90^{\circ}+\frac{1}{2} \angle B D A=\angle B I_{2} A$，可得 $A, B, I_{1}, I_{2}$ 四点共圆．
所以 $\angle B I_{1} l_{2}=180^{\circ}-\angle B A I_{2}=180^{\circ}-\frac{1}{2} \angle B A D$．
同理可得 $\angle B I_{1} P=180^{\circ}-\frac{1}{2} \angle B C D$．
所以 $\angle P I_{1} I_{2}=360^{\circ}-\angle B I_{1} I_{2}-\angle B I_{1} P=90^{\circ}$．
于是 $J_{1}, I_{1}, I_{2}$ 三点共线．
同理 $I_{1}, I_{2}, J_{2}$ 三点共线，从而 $I_{1}, I_{2}, J_{1}, J_{2}$ 四点共线．
由鸡爪关系可得 $QP=QI_1=QJ_1$，从而 $\angle PI_1J_1=90^\circ$．由 $\angle B I_{1} A=90^{\circ}+\frac{1}{2} \angle B C A=90^{\circ}+\frac{1}{2} \angle B D A=\angle B I_{2} A$，可得 $A, B, I_{1}, I_{2}$ 四点共圆．
所以 $\angle B I_{1} l_{2}=180^{\circ}-\angle B A I_{2}=180^{\circ}-\frac{1}{2} \angle B A D$．
同理可得 $\angle B I_{1} P=180^{\circ}-\frac{1}{2} \angle B C D$．
所以 $\angle P I_{1} I_{2}=360^{\circ}-\angle B I_{1} I_{2}-\angle B I_{1} P=90^{\circ}$．
于是 $J_{1}, I_{1}, I_{2}$ 三点共线．
同理 $I_{1}, I_{2}, J_{2}$ 三点共线，从而 $I_{1}, I_{2}, J_{1}, J_{2}$ 四点共线．
答案
解析
备注
