如图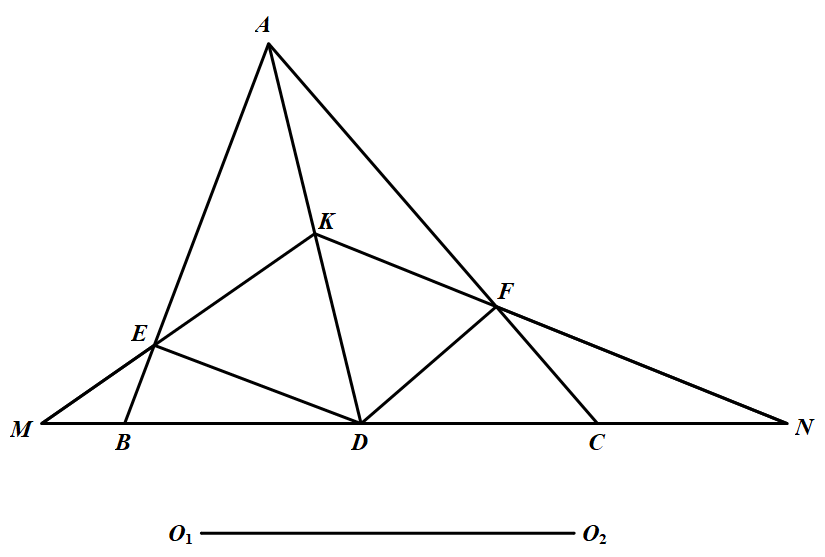
在锐角 $\triangle ABC$ 中，$AB\ne AC$，$K$ 是中线 $AD$ 的中点，$DE\perp AB$ 于点 $E$，$DF \perp AC$ 于点 $ F$，直线 $KE、KF$ 分别与直线 $BC$ 相交于点 $M、N$，$\triangle DEM、\triangle DFN$ 的外心分别为 $O_1,O_2$．证
明：$O_{1} O_{2} \parallel B C$．
在锐角 $\triangle ABC$ 中，$AB\ne AC$，$K$ 是中线 $AD$ 的中点，$DE\perp AB$ 于点 $E$，$DF \perp AC$ 于点 $ F$，直线 $KE、KF$ 分别与直线 $BC$ 相交于点 $M、N$，$\triangle DEM、\triangle DFN$ 的外心分别为 $O_1,O_2$．证明：$O_{1} O_{2} \parallel B C$．
【难度】
【出处】
2017中国东南数学奥林匹克试题(高二)
【标注】
【答案】
略
【解析】
如图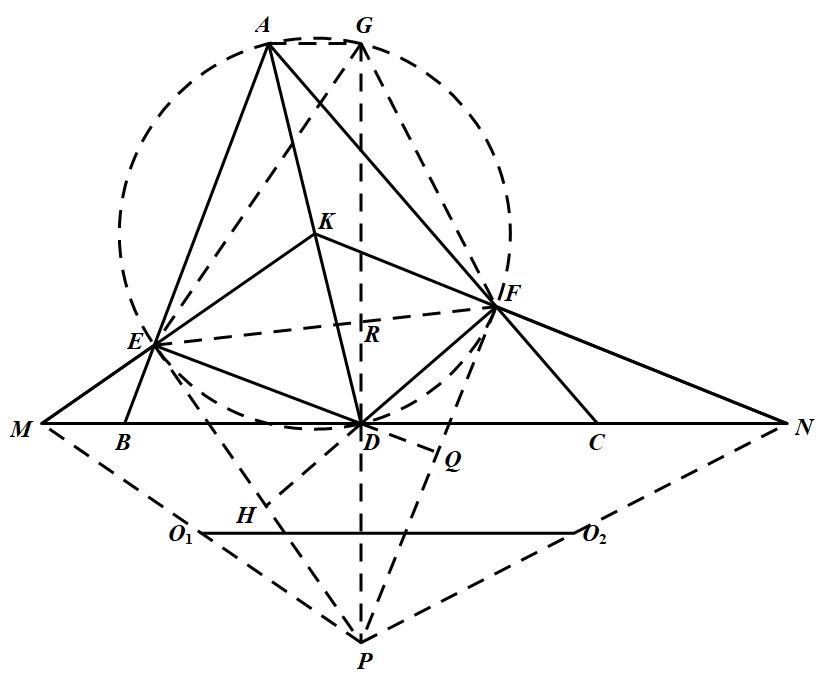
以 $AD$ 为直径作圆 $K$，过点 $A$ 作 $AG \parallel BC$ 与圆 $K$ 交于点 $G$，连结 $ GE、GF$，则 $\angle GAE = 180^\circ-\angle ABC, \angle GAF=\angle ACB$，从而
$\begin{aligned} D E \cdot G F =D B \sin \angle A B C \cdot A D \sin \angle G A F =D B \cdot A D \sin \angle A B C \cdot \sin \angle A C B \\ D F \cdot G E =D C \sin \angle A C B \cdot A D \sin \angle G A E =D C \cdot A D \sin \angle A C B \cdot \sin \angle A B C \end{aligned}$
又 $D B=D C$，所以 $D E \cdot G F=D F \cdot G E$．
过 $E,F$ 分别作圆 $K$ 的切线 $EP,FP$．
设 $EF,DG$ 交于点 $R$，直线 $ED,FD$ 分别与 $FP,EP$ 交于点 $Q,H$，则在 $\triangle DEF$ 中，
$\begin{aligned} & \frac{E R}{R F} \cdot \frac{F H}{H D} \cdot \frac{D Q}{Q E} \\=& \frac{E D \sin \angle E D G}{F D \sin \angle F D G} \cdot \frac{E F \sin \angle F E H}{E D \sin \angle D E H} \cdot \frac{F D \sin \angle Q F D}{E F \sin \angle Q F E} \\=& \frac{\sin \angle E D G \sin \angle F E D}{\sin \angle F D G \sin \angle D F E} \\=& \frac{G E \cdot D F}{G F \cdot D E}=1 \end{aligned}$
（因为 $\angle F E H=\angle Q F E, \angle Q F D=\angle F E D, \angle D E H=\angle D F E$）
由塞瓦定理的逆定理知 $E H、FQ、RD$ 三线共点，即 $G、D、P$ 三点共线．
因为 $D G \perp A G, B C \parallel A G$，所以 $P D \perp B C$．
又 $M E \perp P E$，所以 $P,D,E,M$ 在以 $PM$ 直径的圆上，因此 $\triangle DEM$ 的外心 $O_1$ 是线段 $PM$ 的中点．
同理 $\triangle DFN$ 的外心 $O_2$ 是线段 $PN$ 的中点，所以 $O_1O_2 \parallel MN$，即 $O_1O_2 \parallel BC$．
以 $AD$ 为直径作圆 $K$，过点 $A$ 作 $AG \parallel BC$ 与圆 $K$ 交于点 $G$，连结 $ GE、GF$，则 $\angle GAE = 180^\circ-\angle ABC, \angle GAF=\angle ACB$，从而$\begin{aligned} D E \cdot G F =D B \sin \angle A B C \cdot A D \sin \angle G A F =D B \cdot A D \sin \angle A B C \cdot \sin \angle A C B \\ D F \cdot G E =D C \sin \angle A C B \cdot A D \sin \angle G A E =D C \cdot A D \sin \angle A C B \cdot \sin \angle A B C \end{aligned}$
又 $D B=D C$，所以 $D E \cdot G F=D F \cdot G E$．
过 $E,F$ 分别作圆 $K$ 的切线 $EP,FP$．
设 $EF,DG$ 交于点 $R$，直线 $ED,FD$ 分别与 $FP,EP$ 交于点 $Q,H$，则在 $\triangle DEF$ 中，
$\begin{aligned} & \frac{E R}{R F} \cdot \frac{F H}{H D} \cdot \frac{D Q}{Q E} \\=& \frac{E D \sin \angle E D G}{F D \sin \angle F D G} \cdot \frac{E F \sin \angle F E H}{E D \sin \angle D E H} \cdot \frac{F D \sin \angle Q F D}{E F \sin \angle Q F E} \\=& \frac{\sin \angle E D G \sin \angle F E D}{\sin \angle F D G \sin \angle D F E} \\=& \frac{G E \cdot D F}{G F \cdot D E}=1 \end{aligned}$
（因为 $\angle F E H=\angle Q F E, \angle Q F D=\angle F E D, \angle D E H=\angle D F E$）
由塞瓦定理的逆定理知 $E H、FQ、RD$ 三线共点，即 $G、D、P$ 三点共线．
因为 $D G \perp A G, B C \parallel A G$，所以 $P D \perp B C$．
又 $M E \perp P E$，所以 $P,D,E,M$ 在以 $PM$ 直径的圆上，因此 $\triangle DEM$ 的外心 $O_1$ 是线段 $PM$ 的中点．
同理 $\triangle DFN$ 的外心 $O_2$ 是线段 $PN$ 的中点，所以 $O_1O_2 \parallel MN$，即 $O_1O_2 \parallel BC$．
答案
解析
备注
