如图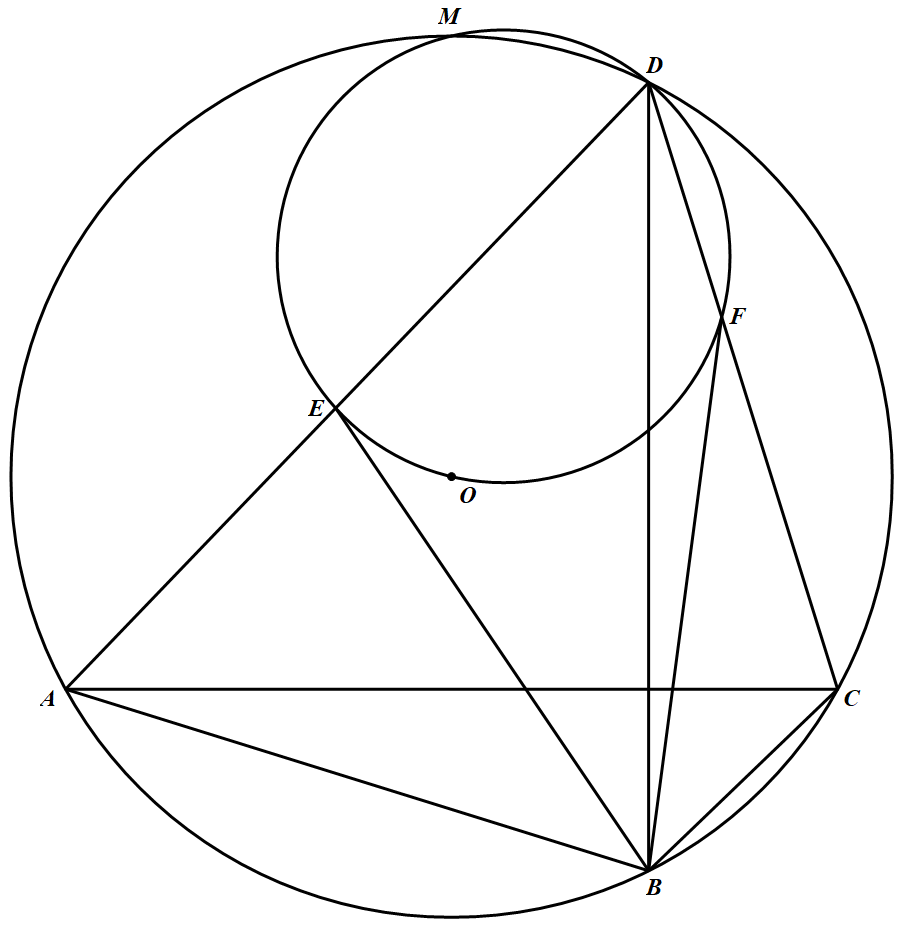
在圆 $O$ 的内接四边形 $ABCD$ 中，对角线 $AC、BD$ 互相垂直，弧 $\overparen{ADC}$ 的中点为 $M$，过 $M,O,D$ 三点的圆与 $DA,DC$ 分别
交于点 $E、F$．证明：$BE= BF$．
在圆 $O$ 的内接四边形 $ABCD$ 中，对角线 $AC、BD$ 互相垂直，弧 $\overparen{ADC}$ 的中点为 $M$，过 $M,O,D$ 三点的圆与 $DA,DC$ 分别交于点 $E、F$．证明：$BE= BF$．
【难度】
【出处】
2017中国东南数学奥林匹克试题(高二)
【标注】
【答案】
略
【解析】
如图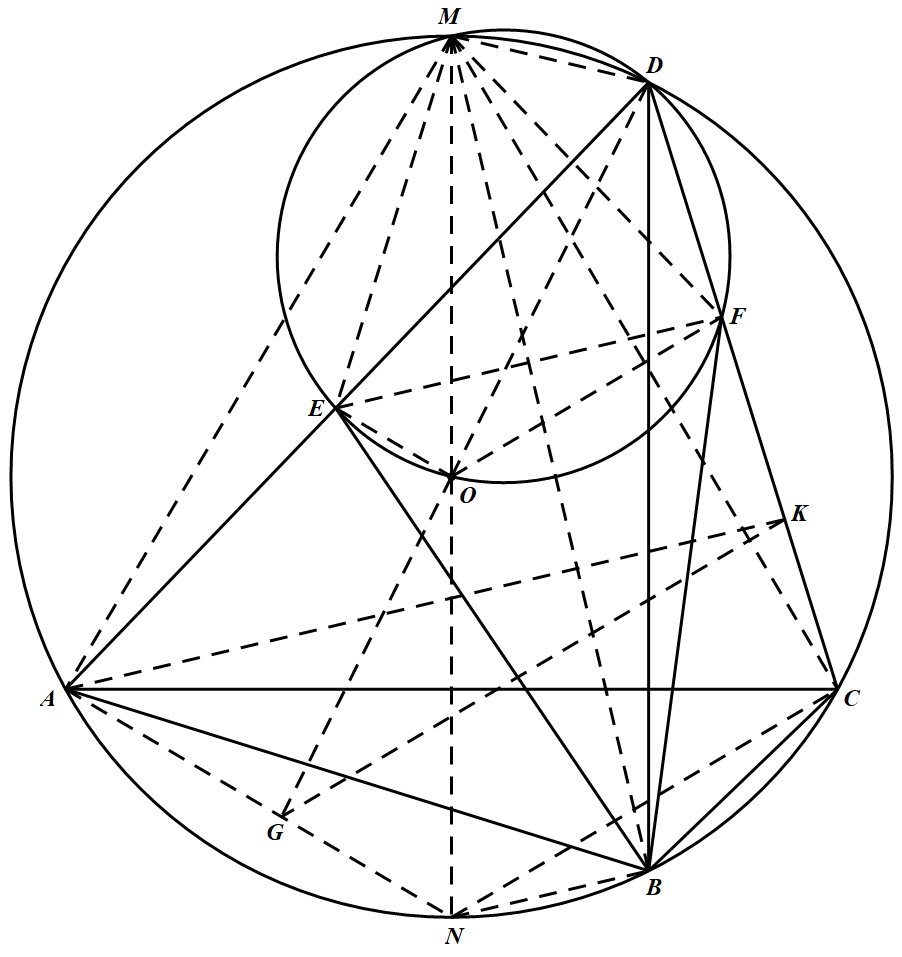
连结 $ME、MF、MD、MA、MB、MC、EF$．由 $M,E,O,F,D$ 共圆知，
$\begin{aligned} \angle M F E &=\angle M D E=\angle M D A=\angle M C A \\\angle M E F &=180^{\circ}-\angle M D F=180^{\circ}-\angle M D C =\angle M A C \end{aligned}$
又由 $M$ 为弧 $\overparen{ADC}$ 的中点知 $\angle MCA=\angle MAC$，所以 $\angle M F E=\angle M E F$，从而 $M E=M F$．
设直线 $MO$ 与圆 $O$ 交于另一点 $N$，连结 $OE,OF,NA,NC$，则 $\angle D E O=\angle D M O=\angle D M N=\angle D A N$，所以 $OE\parallel AN$，同理 $OF \parallel N C$．
连结 $DO$，并延长与 $AN$ 相交于点 $G$，过 $G$ 作 $GK\parallel NC$ 与 $DC$ 相交于点 $K$，则 $\triangle AGK$ 与 $\triangle EOF$ 是位似三角形，位似中心为 $D$，从而 $EF\parallel AK$．
由 $GK\parallel NC$ 及 $A,N,C,D$ 四点共圆知，$\angle A G K=\angle A N C=180^{\circ}-\angle A D C$，故 $A、G、K、D$ 四点共圆，从而 $\angle AKG=\angle ADG$．又 $DB\bot AC$，所以 $\angle BDC＝90^\circ-\angle ACD= \angle ADG$，从而 $\angle BNC=\angle BDC=\angle ADC=\angle AKG$，结合 $GK \parallel NC$ 可知，$NB\parallel AK$．又由 $MN$ 为圆 $O$ 的直径知，$BM\bot NB$，从而 $BM\bot AK$．于是 $BM\bot EF$．
因此，$BM$ 是线段 $EF$ 的垂直平分线，从而 $BE=BF$．
连结 $ME、MF、MD、MA、MB、MC、EF$．由 $M,E,O,F,D$ 共圆知，$\begin{aligned} \angle M F E &=\angle M D E=\angle M D A=\angle M C A \\\angle M E F &=180^{\circ}-\angle M D F=180^{\circ}-\angle M D C =\angle M A C \end{aligned}$
又由 $M$ 为弧 $\overparen{ADC}$ 的中点知 $\angle MCA=\angle MAC$，所以 $\angle M F E=\angle M E F$，从而 $M E=M F$．
设直线 $MO$ 与圆 $O$ 交于另一点 $N$，连结 $OE,OF,NA,NC$，则 $\angle D E O=\angle D M O=\angle D M N=\angle D A N$，所以 $OE\parallel AN$，同理 $OF \parallel N C$．
连结 $DO$，并延长与 $AN$ 相交于点 $G$，过 $G$ 作 $GK\parallel NC$ 与 $DC$ 相交于点 $K$，则 $\triangle AGK$ 与 $\triangle EOF$ 是位似三角形，位似中心为 $D$，从而 $EF\parallel AK$．
由 $GK\parallel NC$ 及 $A,N,C,D$ 四点共圆知，$\angle A G K=\angle A N C=180^{\circ}-\angle A D C$，故 $A、G、K、D$ 四点共圆，从而 $\angle AKG=\angle ADG$．又 $DB\bot AC$，所以 $\angle BDC＝90^\circ-\angle ACD= \angle ADG$，从而 $\angle BNC=\angle BDC=\angle ADC=\angle AKG$，结合 $GK \parallel NC$ 可知，$NB\parallel AK$．又由 $MN$ 为圆 $O$ 的直径知，$BM\bot NB$，从而 $BM\bot AK$．于是 $BM\bot EF$．
因此，$BM$ 是线段 $EF$ 的垂直平分线，从而 $BE=BF$．
答案
解析
备注
