平面上的四个点，若以其中每三点为顶点的三角形的面积为 $4$ 个互不相同的正整数，并且其中每两点之间的距离为 $6$ 个互不相同的正整数，则称这四个点的凸包为一个"莲花图"．
（1）试给出一个具体的"莲花图"，同时给出相应的 $4$ 个三角形的面积及每对顶点之间的距离；
（2）证明：平面上存在无穷多个互不相似的"莲花图"．
注：对平面上不共线的有限个点所组成的集合 $S$，其凸包为一个凸多边形区域 $\Omega$（含边界及内部）：$\Omega$ 的每个顶点都是 $S$ 中的点，$S$ 中的每个点都属于 $\Omega$．
（1）试给出一个具体的"莲花图"，同时给出相应的 $4$ 个三角形的面积及每对顶点之间的距离；
（2）证明：平面上存在无穷多个互不相似的"莲花图"．
注：对平面上不共线的有限个点所组成的集合 $S$，其凸包为一个凸多边形区域 $\Omega$（含边界及内部）：$\Omega$ 的每个顶点都是 $S$ 中的点，$S$ 中的每个点都属于 $\Omega$．
【难度】
【出处】
2016中国东南数学奥林匹克试题(高一)
【标注】
【答案】
略
【解析】
（1）下图中所示的两个完全四边形 $ABCD$，它由四个边长为整数的直角三角形拼接而成，由于每个直角三角形的边长及面积皆为整数，所拼得的四边形六条边长为互异正整数，面积之值也为互异正整数，故这两个四边形皆是莲花图．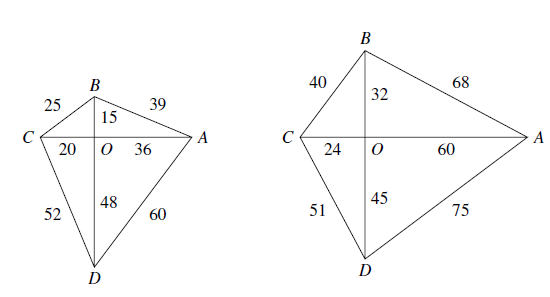
（2）任取两组勾股数 $(a,b,c)$ 及 $(x,y,z)$，其中 $a^2 + b^2 = c^2 ,~ x^2 + y^2 = z^2$，作对角线相互垂直于 $O$ 的凸四边形 $ABCD$，使得 $OA=ay,~OB=ax,~OC=bx,~OD=by$．
由勾股定理可知，$AB=az$，$BC=cx$，$CD=bz$，$DA=cy$，因此，$A,B,C,D$ 中任意两点之间的距离为正整数．又由勾股数性质知，$a,b$ 中必有一个偶数，$x,y$ 中必有一个偶数，从而 $\triangle AOB,\triangle BOC,\triangle COD,\triangle DOA$ 这四个直角三角形的面积均为整数，于是 $\triangle ABC,\triangle BCD,\triangle CDA,\triangle DAB$ 的面积必为正整数．将这样的凸四边形 $ABCD$ 记为 $Q(a,b,c,x,y,z)$．
对任意整数 $t>1$，注意到 $(2t,t^2 -1,t^2 +1)$ 为勾股数组，令 $Q_t = Q(3,4,5,2t,t^2 -1,t^2 +1)=A_t B_t C_t D_t$
我们证明：存在无穷多个整数 $t>1$，使得 $Q_t$ 的凸包为莲花图．令$$\begin{aligned}
&\left\{ \begin{aligned} f_1 (t) &= A_t B_t = 3t^2 +3 \\ f_2 (t) &= B_t C_t = 10t \\ f_3 (t) &= C_t D_t = 4t^2 +4 \\ f_4 (t) &= D_t A_t = 5t^2 -5 \\ f_5 (t) &= A_t C_t = 3t^2 +8t-3 \\ f_6 (t) &= B_t D_t = 4t^2 +6t-4 \end{aligned} \right.\\
&\left\{ \begin{aligned} g_1 (t) &= S_{\triangle A_t B_t C_t}=3t(3t^2 + 8t-3) \\ g_2 (t) &= S_{\triangle B_t C_t D_t}=4t(4t^2 +6t-4) \\ g_3 (t) &= S_{\triangle C_t D_t A_t}=(2t^2 -2)(3t^2 +8t-3) \\ g_4 (t) &= S_{\triangle D_t A_t B_t}=(3t^2 -3)(2t^2 +3t-2) \end{aligned} \right.
\end{aligned}$$对任意一组 $(i,j)$（$1\leqslant i<j\leqslant 6$），满足方程 $f_i (t)=f_j (t)$ 的正整数 $t$ 不多于 $2$ 个，又对任意一组 $(i,j)$
（$1\leqslant i<j\leqslant 4$），满足方程 $g_i (t)=g_j (t)$ 的正整数 $t$ 不多于 $2$ 个．因此，存在一个无穷集 $T\subset \mathbb{N}_{+}\backslash \{1\}$，使得对每个固定的 $t\in T$，各 $f_k (t)$（$k=1,2,\ldots,6$）互不相等，且各 $g_l (t)$（$l=1,2,3,4$）互不相等，此时 $Q$ 符合莲花图的条件．
再证明 $\{Q_t ~|~ t\in T\}$ 中存在无穷多个互不相似的四边形．
事实上，当 $t>3$ 时，易知 $Q_t$ 的最长边与最短边之比为
$\varphi (t)=\dfrac{D_t A_t}{B_t C_t}=\dfrac{5t^2 -5}{10t}=\dfrac{1}{2}\left(t-\dfrac{1}{t}\right)$
由 $\varphi (t)$ 的单调性可知，对任意 $t_1 , t_2 \in T$，
$3<t_1 <t_2$，有 $\varphi(t_1 )<\varphi(t_2 )$，从而 $Q_{t_1}$ 与 $Q_{t_2}$ 不相似．
因此，存在无穷多个互不相似的莲花图．
（2）任取两组勾股数 $(a,b,c)$ 及 $(x,y,z)$，其中 $a^2 + b^2 = c^2 ,~ x^2 + y^2 = z^2$，作对角线相互垂直于 $O$ 的凸四边形 $ABCD$，使得 $OA=ay,~OB=ax,~OC=bx,~OD=by$．由勾股定理可知，$AB=az$，$BC=cx$，$CD=bz$，$DA=cy$，因此，$A,B,C,D$ 中任意两点之间的距离为正整数．又由勾股数性质知，$a,b$ 中必有一个偶数，$x,y$ 中必有一个偶数，从而 $\triangle AOB,\triangle BOC,\triangle COD,\triangle DOA$ 这四个直角三角形的面积均为整数，于是 $\triangle ABC,\triangle BCD,\triangle CDA,\triangle DAB$ 的面积必为正整数．将这样的凸四边形 $ABCD$ 记为 $Q(a,b,c,x,y,z)$．
对任意整数 $t>1$，注意到 $(2t,t^2 -1,t^2 +1)$ 为勾股数组，令 $Q_t = Q(3,4,5,2t,t^2 -1,t^2 +1)=A_t B_t C_t D_t$
我们证明：存在无穷多个整数 $t>1$，使得 $Q_t$ 的凸包为莲花图．令$$\begin{aligned}
&\left\{ \begin{aligned} f_1 (t) &= A_t B_t = 3t^2 +3 \\ f_2 (t) &= B_t C_t = 10t \\ f_3 (t) &= C_t D_t = 4t^2 +4 \\ f_4 (t) &= D_t A_t = 5t^2 -5 \\ f_5 (t) &= A_t C_t = 3t^2 +8t-3 \\ f_6 (t) &= B_t D_t = 4t^2 +6t-4 \end{aligned} \right.\\
&\left\{ \begin{aligned} g_1 (t) &= S_{\triangle A_t B_t C_t}=3t(3t^2 + 8t-3) \\ g_2 (t) &= S_{\triangle B_t C_t D_t}=4t(4t^2 +6t-4) \\ g_3 (t) &= S_{\triangle C_t D_t A_t}=(2t^2 -2)(3t^2 +8t-3) \\ g_4 (t) &= S_{\triangle D_t A_t B_t}=(3t^2 -3)(2t^2 +3t-2) \end{aligned} \right.
\end{aligned}$$对任意一组 $(i,j)$（$1\leqslant i<j\leqslant 6$），满足方程 $f_i (t)=f_j (t)$ 的正整数 $t$ 不多于 $2$ 个，又对任意一组 $(i,j)$
（$1\leqslant i<j\leqslant 4$），满足方程 $g_i (t)=g_j (t)$ 的正整数 $t$ 不多于 $2$ 个．因此，存在一个无穷集 $T\subset \mathbb{N}_{+}\backslash \{1\}$，使得对每个固定的 $t\in T$，各 $f_k (t)$（$k=1,2,\ldots,6$）互不相等，且各 $g_l (t)$（$l=1,2,3,4$）互不相等，此时 $Q$ 符合莲花图的条件．
再证明 $\{Q_t ~|~ t\in T\}$ 中存在无穷多个互不相似的四边形．
事实上，当 $t>3$ 时，易知 $Q_t$ 的最长边与最短边之比为
$\varphi (t)=\dfrac{D_t A_t}{B_t C_t}=\dfrac{5t^2 -5}{10t}=\dfrac{1}{2}\left(t-\dfrac{1}{t}\right)$
由 $\varphi (t)$ 的单调性可知，对任意 $t_1 , t_2 \in T$，
$3<t_1 <t_2$，有 $\varphi(t_1 )<\varphi(t_2 )$，从而 $Q_{t_1}$ 与 $Q_{t_2}$ 不相似．
因此，存在无穷多个互不相似的莲花图．
答案
解析
备注
