如图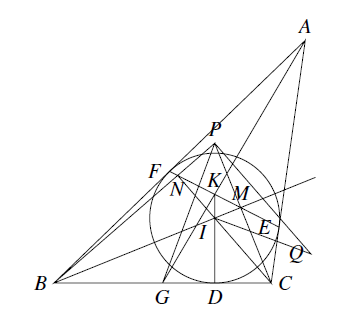
$\triangle ABC$ 的内切圆 $I$ 与边 $BC,CA,AB$ 分别切于点 $D,E,F$，直线 $BI,CI,DI$ 分别与 $EF$ 交于点 $M,N,K$，直线 $BN$ 与 $CM$ 交于点 $P$，直线 $AK$ 与 $BC$ 交于点 $G$，过点 $I$ 垂直于 $PG$ 的直线与过点 $P$ 垂直于 $PB$ 的直线交于点 $Q$．证明：直线 $BI$ 平分线段 $PQ$．
$\triangle ABC$ 的内切圆 $I$ 与边 $BC,CA,AB$ 分别切于点 $D,E,F$，直线 $BI,CI,DI$ 分别与 $EF$ 交于点 $M,N,K$，直线 $BN$ 与 $CM$ 交于点 $P$，直线 $AK$ 与 $BC$ 交于点 $G$，过点 $I$ 垂直于 $PG$ 的直线与过点 $P$ 垂直于 $PB$ 的直线交于点 $Q$．证明：直线 $BI$ 平分线段 $PQ$．【难度】
【出处】
2016中国东南数学奥林匹克试题(高一)
【标注】
【答案】
略
【解析】
如图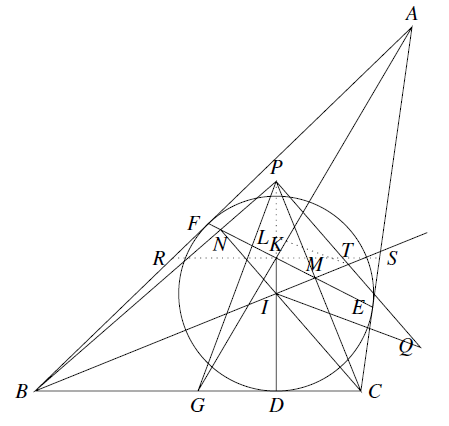
过点 $K$ 作平行于 $BC$ 的直线分别与 $AB,AC$ 交于点 $R,S$，则 $IK\perp RS$，又 $IF \perp AB$，所以 $I,K,F,R$ 四点共圆，同理 $I,K,S,E$ 四点共圆，所以 $\angle IRK=\angle IFK=\angle IEK=\angle ISK$，从而 $KR=KS$．由 $RS\parallel BC$ 知，$G$ 为 $BC$ 的中点．
因为 $\begin{aligned}\angle CNE&=\angle AEF-\angle ECN=90^{\circ}-\frac{\angle BAC}{2}-\frac{\angle ACB}{2} =\frac{\angle ABC}{2}=\angle FBI \end{aligned}$
所以 $B,I,N,F$ 四点共圆，又易知 $B,D,I,F$ 四点共圆，所以 $B,D,I,N,F$ 五点共圆．从而 $IN\perp BN$，同理 $IM\perp CM$．所以 $I$ 为 $\triangle PBC$ 的垂心，进而有 $PI\perp BC$，
于是 $P,I,D$ 共线．
设 $BI$ 与 $PQ$ 交于点 $T$．
由 $D,C,M,I$ 四点共圆知，$\angle PIM=\angle PCB$，又 $\angle TPI=90^{\circ}-\angle BPD=\angle PBC$，所以 $\triangle TPI\sim\triangle PBC$．
取 $PI$ 中点 $L$，则 $\triangle TPL\sim\triangle PBG$，于是 $\angle PTL=\angle BPG$，所以 $\angle PTL+\angle GPT=\angle BPG+\angle GPT=\angle BPQ=90^{\circ}$，从而 $TL\parallel QI$．
因此 $PT=TQ$，即 $BI$ 平分 $PQ$．
过点 $K$ 作平行于 $BC$ 的直线分别与 $AB,AC$ 交于点 $R,S$，则 $IK\perp RS$，又 $IF \perp AB$，所以 $I,K,F,R$ 四点共圆，同理 $I,K,S,E$ 四点共圆，所以 $\angle IRK=\angle IFK=\angle IEK=\angle ISK$，从而 $KR=KS$．由 $RS\parallel BC$ 知，$G$ 为 $BC$ 的中点．因为 $\begin{aligned}\angle CNE&=\angle AEF-\angle ECN=90^{\circ}-\frac{\angle BAC}{2}-\frac{\angle ACB}{2} =\frac{\angle ABC}{2}=\angle FBI \end{aligned}$
所以 $B,I,N,F$ 四点共圆，又易知 $B,D,I,F$ 四点共圆，所以 $B,D,I,N,F$ 五点共圆．从而 $IN\perp BN$，同理 $IM\perp CM$．所以 $I$ 为 $\triangle PBC$ 的垂心，进而有 $PI\perp BC$，
于是 $P,I,D$ 共线．
设 $BI$ 与 $PQ$ 交于点 $T$．
由 $D,C,M,I$ 四点共圆知，$\angle PIM=\angle PCB$，又 $\angle TPI=90^{\circ}-\angle BPD=\angle PBC$，所以 $\triangle TPI\sim\triangle PBC$．
取 $PI$ 中点 $L$，则 $\triangle TPL\sim\triangle PBG$，于是 $\angle PTL=\angle BPG$，所以 $\angle PTL+\angle GPT=\angle BPG+\angle GPT=\angle BPQ=90^{\circ}$，从而 $TL\parallel QI$．
因此 $PT=TQ$，即 $BI$ 平分 $PQ$．
答案
解析
备注
