在 $\triangle ABC$ 中，$AB>AC$，$I$ 为 $\triangle ABC$ 的内心．用 $\Gamma$ 表示以 $AI$ 为直径的圆．设 $\Gamma$ 与 $\triangle ABC$ 的外接圆交于点 $A$ 与 $D$，且 $D$ 在不含点 $B$ 的弧 $\overparen{AC}$ 上，过点 $A$ 作 $BC$ 的平行线，与圆 $\Gamma$ 交于 $A$ 及另一点 $E$（如图所示）．若 $DI$ 平分 $\angle CDE$，且 $\angle ABC=33^{\circ}$，求 $\angle BAC$ 的度数．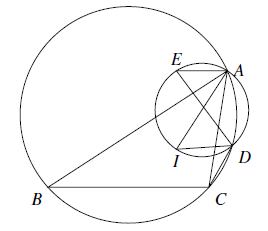
【难度】
【出处】
2015中国东南数学奥林匹克试题(高二)
【标注】
【答案】
略
【解析】
用 $\Gamma_1$ 表示 $\triangle ABC$ 的外接圆．延长 $AI$ 交 $\Gamma_1$ 于点 $M$，延长 $DE$ 交 $\Gamma_1$ 于点 $N$，连结 $AD,EI,MN$（如图所示）．由 $A,D,I,E$ 四点共圆，以及 $A,D,M,N$ 四点共圆，可得
$\angle AIE=\angle ADE=\angle ADN=\angle AMN$，故 $EI\parallel MN$．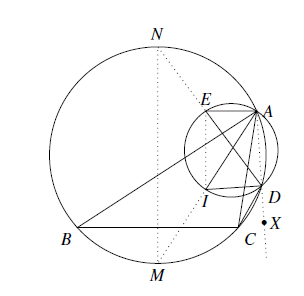
由 $AI$ 为圆 $\Gamma$ 的直径知，$EI\perp AE$，而 $AE\parallel BC$，
所以 $EI\perp BC$，从而 $MN\perp BC$．
注意到 $I$ 为 $\triangle ABC$ 的内心，故 $M$ 为弧 $\overparen{BC}$（不含 $A$）的中点，于是 $N$ 为弧 $\overparen{BAC}$ 的中点，即 $\overparen{NB}=\overparen{NC}$ 。
将 $AD$ 延长线上任意一点记为 $X$．
由条件知，$ID\perp AX$，故由 $DI$ 平分 $\angle CDE$ 可知，$\angle ADE=\angle CDX=\angle ABC$，从而 $\overparen{NA}=\overparen{AC}$，
进而有 $\overparen{ANB}=\overparen{NB}+\overparen{NA}=\overparen{NC}+\overparen{NA}=3\overparen{AC}$
所以 $\angle ACB=3\angle ABC$ 。
再根据 $\angle ABC=33^{\circ}$ 可知，
$\begin{aligned} \angle B A C &=180^{\circ}-\angle A B C-\angle A C B \\ &=180^{\circ}-4 \times 33^{\circ} \\ &=48^{\circ} \end{aligned}$
$\angle AIE=\angle ADE=\angle ADN=\angle AMN$，故 $EI\parallel MN$．
由 $AI$ 为圆 $\Gamma$ 的直径知，$EI\perp AE$，而 $AE\parallel BC$，所以 $EI\perp BC$，从而 $MN\perp BC$．
注意到 $I$ 为 $\triangle ABC$ 的内心，故 $M$ 为弧 $\overparen{BC}$（不含 $A$）的中点，于是 $N$ 为弧 $\overparen{BAC}$ 的中点，即 $\overparen{NB}=\overparen{NC}$ 。
将 $AD$ 延长线上任意一点记为 $X$．
由条件知，$ID\perp AX$，故由 $DI$ 平分 $\angle CDE$ 可知，$\angle ADE=\angle CDX=\angle ABC$，从而 $\overparen{NA}=\overparen{AC}$，
进而有 $\overparen{ANB}=\overparen{NB}+\overparen{NA}=\overparen{NC}+\overparen{NA}=3\overparen{AC}$
所以 $\angle ACB=3\angle ABC$ 。
再根据 $\angle ABC=33^{\circ}$ 可知，
$\begin{aligned} \angle B A C &=180^{\circ}-\angle A B C-\angle A C B \\ &=180^{\circ}-4 \times 33^{\circ} \\ &=48^{\circ} \end{aligned}$
答案
解析
备注
