如图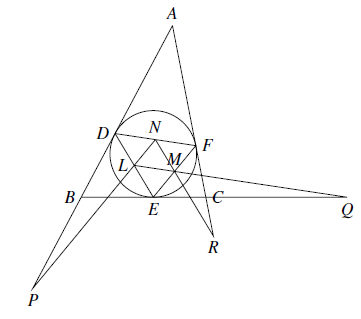
在 $\triangle ABC$ 中，$AB>AC>BC$．$\triangle ABC$ 的内切圆与边 $AB,BC,CA$ 分别相切于点 $D,E,F$，线段 $DE,EF,FD$ 的中点分别是 $L,M,N$．直线 $NL$ 与射线 $AB$ 交于点 $P$，直线 $LM$ 与射线 $BC$ 交于点 $Q$，直线 $NM$ 与射线 $AC$ 交于点 $R$．证明：$PA \cdot QB \cdot RC = PD \cdot QE \cdot RF$
在 $\triangle ABC$ 中，$AB>AC>BC$．$\triangle ABC$ 的内切圆与边 $AB,BC,CA$ 分别相切于点 $D,E,F$，线段 $DE,EF,FD$ 的中点分别是 $L,M,N$．直线 $NL$ 与射线 $AB$ 交于点 $P$，直线 $LM$ 与射线 $BC$ 交于点 $Q$，直线 $NM$ 与射线 $AC$ 交于点 $R$．证明：$PA \cdot QB \cdot RC = PD \cdot QE \cdot RF$【难度】
【出处】
2015中国东南数学奥林匹克试题(高二)
【标注】
【答案】
略
【解析】
设直线 $DE$ 与 $AR$ 交于点 $S$，如图，则由梅内劳斯（Menelaus）定理知
$
\dfrac{A D}{D B} \cdot \dfrac{B E}{E C} \cdot \dfrac{C S}{S A}=1
$．
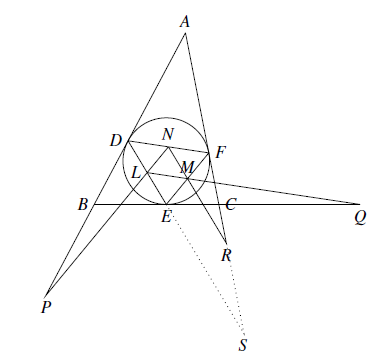又 $AD=AF,DB=BE,EC=CF$，所以 $\dfrac{C S}{C F}=\dfrac{S A}{A F}$ ①
注意到 $M,N$ 分别为 $EF,FD$ 的中点，故 $R$ 为 $FS$ 的中点，从而有
$CS-CF=2RC,~SA-AF=2RF$，结合 ① 可知，
$
\dfrac{2 R C}{C F}=\dfrac{C S-C F}{C F}=\dfrac{S A-A F}{A F}=\dfrac{2 R F}{A F}
$
即
$
\dfrac{R C}{C F}=\dfrac{R F}{A F}
$．
进而得
$
\dfrac{R C}{R F}=\dfrac{R C}{R C+C F}=\dfrac{R F}{R F+A F}=\dfrac{R F}{R A}
$
即
$
R F^{2}=R C \cdot R A
$．
同理可知
$
P D^{2}=P A \cdot P B,~ Q E^{2}=Q B \cdot Q C
$．
所以点 $P,Q,R$ 均是 $\triangle ABC$ 的内切圆和外接圆的等幂点，从而 $P,Q,R$ 三点共线．
由梅内劳斯定理得
$
\dfrac{A P}{P B} \cdot \dfrac{B Q}{Q C} \cdot \dfrac{C R}{R A}=1
$，
故
$\begin{aligned} \frac{A P^{2}}{P D^{2}} \cdot \frac{B Q^{2}}{Q E^{2}} \cdot \frac{C R^{2}}{R F^{2}} &=\frac{A P^{2}}{P A \cdot P B} \cdot \frac{B Q^{2}}{Q B \cdot Q C} \cdot \frac{C R^{2}}{R C \cdot R A} \\ &=\frac{A P}{P B} \cdot \frac{B Q}{Q C} \cdot \frac{C R}{R A} \\ &=1 \end{aligned}$
即
$
P A \cdot Q B \cdot R C=P D \cdot Q E \cdot R F
$．
$
\dfrac{A D}{D B} \cdot \dfrac{B E}{E C} \cdot \dfrac{C S}{S A}=1
$．
又 $AD=AF,DB=BE,EC=CF$，所以 $\dfrac{C S}{C F}=\dfrac{S A}{A F}$ ①注意到 $M,N$ 分别为 $EF,FD$ 的中点，故 $R$ 为 $FS$ 的中点，从而有
$CS-CF=2RC,~SA-AF=2RF$，结合 ① 可知，
$
\dfrac{2 R C}{C F}=\dfrac{C S-C F}{C F}=\dfrac{S A-A F}{A F}=\dfrac{2 R F}{A F}
$
即
$
\dfrac{R C}{C F}=\dfrac{R F}{A F}
$．
进而得
$
\dfrac{R C}{R F}=\dfrac{R C}{R C+C F}=\dfrac{R F}{R F+A F}=\dfrac{R F}{R A}
$
即
$
R F^{2}=R C \cdot R A
$．
同理可知
$
P D^{2}=P A \cdot P B,~ Q E^{2}=Q B \cdot Q C
$．
所以点 $P,Q,R$ 均是 $\triangle ABC$ 的内切圆和外接圆的等幂点，从而 $P,Q,R$ 三点共线．
由梅内劳斯定理得
$
\dfrac{A P}{P B} \cdot \dfrac{B Q}{Q C} \cdot \dfrac{C R}{R A}=1
$，
故
$\begin{aligned} \frac{A P^{2}}{P D^{2}} \cdot \frac{B Q^{2}}{Q E^{2}} \cdot \frac{C R^{2}}{R F^{2}} &=\frac{A P^{2}}{P A \cdot P B} \cdot \frac{B Q^{2}}{Q B \cdot Q C} \cdot \frac{C R^{2}}{R C \cdot R A} \\ &=\frac{A P}{P B} \cdot \frac{B Q}{Q C} \cdot \frac{C R}{R A} \\ &=1 \end{aligned}$
即
$
P A \cdot Q B \cdot R C=P D \cdot Q E \cdot R F
$．
答案
解析
备注
