如图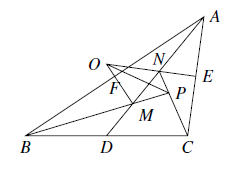
在钝角 $\triangle ABC$ 中，$AB>AC$，点 $O$ 是其外心，边 $BC,CA,AB$ 的中点分别为 $D,E,F$，中线 $AD$ 与 $OF,OE$ 所在直线分别交于点 $M,N$，直线 $BM,CN$ 交于点 $P$．证明：$OP\perp AP$
在钝角 $\triangle ABC$ 中，$AB>AC$，点 $O$ 是其外心，边 $BC,CA,AB$ 的中点分别为 $D,E,F$，中线 $AD$ 与 $OF,OE$ 所在直线分别交于点 $M,N$，直线 $BM,CN$ 交于点 $P$．证明：$OP\perp AP$【难度】
【出处】
2014中国东南数学奥林匹克试题(高一)
【标注】
【答案】
略
【解析】
由已知得，$BM=AM$，$CN=AN$，$\angle AMP=2\angle BAM$，$\angle PND=2\angle CAM$．
如图，连结 $OB,OC$．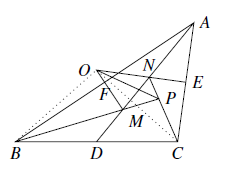
由于 $O$ 是 $\triangle ABC$ 外心，故
$\begin{aligned} \angle B O C=2 \angle B A C &=2 \angle B A M+2 \angle C A M =\angle A M P+\angle P N D=\angle B P C \end{aligned}$
因此 $B,O,P,C$ 四点共圆，所以
$\angle BPO=\angle BCO=\angle CBO=\angle OPN$．
另一方面，对 $\triangle BCP$ 及截线 $DMN$ 用梅涅劳斯定理，得
$
\dfrac{B D}{D C} \cdot \dfrac{C N}{N P} \cdot \dfrac{P M}{M B}=1
$，
结合 $BD=DC$，$BM=AM$，$CN=AN$ 可知，
$
\dfrac{P M}{P N}=\dfrac{M B}{N C}=\dfrac{A M}{A N}
$
即 $PA$ 是 $\angle MPN$ 的外角平分线．又 $PO$ 是 $\angle MPN$ 的平分线，故 $OP \perp AP$．
如图，连结 $OB,OC$．
由于 $O$ 是 $\triangle ABC$ 外心，故$\begin{aligned} \angle B O C=2 \angle B A C &=2 \angle B A M+2 \angle C A M =\angle A M P+\angle P N D=\angle B P C \end{aligned}$
因此 $B,O,P,C$ 四点共圆，所以
$\angle BPO=\angle BCO=\angle CBO=\angle OPN$．
另一方面，对 $\triangle BCP$ 及截线 $DMN$ 用梅涅劳斯定理，得
$
\dfrac{B D}{D C} \cdot \dfrac{C N}{N P} \cdot \dfrac{P M}{M B}=1
$，
结合 $BD=DC$，$BM=AM$，$CN=AN$ 可知，
$
\dfrac{P M}{P N}=\dfrac{M B}{N C}=\dfrac{A M}{A N}
$
即 $PA$ 是 $\angle MPN$ 的外角平分线．又 $PO$ 是 $\angle MPN$ 的平分线，故 $OP \perp AP$．
答案
解析
备注
