如图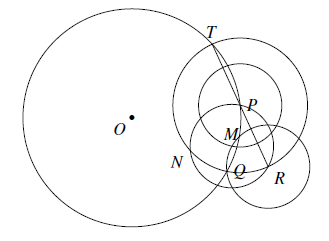
设 $O$ 为平面上一个定圆 $\omega_1$ 的圆心，$P$ 为圆周上一个动点，以 $P$ 为圆心，作半径小于圆 $O$ 半径的圆 $\omega_2$，交 $\omega_1$ 于 $T,Q$，设 $TR$ 为 $\omega_2$ 的直径．分别以 $R,P$ 为圆心，$RQ$ 为半径作圆，设两圆与 $Q$ 在直线 $PR$ 同侧的交点为 $M$．以 $M$ 为圆心，$MR$ 为半径的圆与 $\omega_2$ 交于 $R,N$．证明：以 $T$ 为圆心，$TN$ 为半径的圆过点 $O$．
设 $O$ 为平面上一个定圆 $\omega_1$ 的圆心，$P$ 为圆周上一个动点，以 $P$ 为圆心，作半径小于圆 $O$ 半径的圆 $\omega_2$，交 $\omega_1$ 于 $T,Q$，设 $TR$ 为 $\omega_2$ 的直径．分别以 $R,P$ 为圆心，$RQ$ 为半径作圆，设两圆与 $Q$ 在直线 $PR$ 同侧的交点为 $M$．以 $M$ 为圆心，$MR$ 为半径的圆与 $\omega_2$ 交于 $R,N$．证明：以 $T$ 为圆心，$TN$ 为半径的圆过点 $O$．【难度】
【出处】
2014中国东南数学奥林匹克试题(高一)
【标注】
【答案】
略
【解析】
如图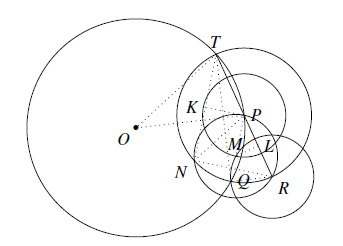
设 $\angle QTR=\alpha$．由条件得：$\overparen{TP}=\overparen{PQ}$，所以 $\angle TOP=2\angle TQP=2\angle QTR=2\alpha$．
设 $QR=x$，$TP=r$，则 $
\dfrac{x}{2 r}=\dfrac{Q R}{T R}=\sin \alpha=\dfrac{\frac{T P}{2}}{O T}=\dfrac{\frac{r}{2}}{O T}
$，
由此得到 $OT=\dfrac{r^2}{x}$．
作 $PK\perp TN$ 于点 $K$，$ML\perp TR$ 于点 $L$，则
$\angle TPK=\angle KPN$ ①
注意到 $NM=PM=RM=QR=x$，所以 $\triangle PNM\cong\triangle PRM$，因此
$\angle N P M=\angle R P M$ ②
由 ①，② 知，$\angle KPN+\angle NPM=90^{\circ}$，而 $\angle PML+\angle NPM=\angle PML+\angle RPM=90^{\circ}$，
故 $\angle KPN=\angle PML$．因此
$
\dfrac{\frac{T N}{2}}{r}=\sin \angle K P N=\sin \angle P M L=\dfrac{\frac{r}{2}}{x}
$
从而 $TN=\dfrac{r^2}{x}=OT$，即以 $T$ 为圆心，$TN$ 为半径的圆过点 $O$．
设 $\angle QTR=\alpha$．由条件得：$\overparen{TP}=\overparen{PQ}$，所以 $\angle TOP=2\angle TQP=2\angle QTR=2\alpha$．设 $QR=x$，$TP=r$，则 $
\dfrac{x}{2 r}=\dfrac{Q R}{T R}=\sin \alpha=\dfrac{\frac{T P}{2}}{O T}=\dfrac{\frac{r}{2}}{O T}
$，
由此得到 $OT=\dfrac{r^2}{x}$．
作 $PK\perp TN$ 于点 $K$，$ML\perp TR$ 于点 $L$，则
$\angle TPK=\angle KPN$ ①
注意到 $NM=PM=RM=QR=x$，所以 $\triangle PNM\cong\triangle PRM$，因此
$\angle N P M=\angle R P M$ ②
由 ①，② 知，$\angle KPN+\angle NPM=90^{\circ}$，而 $\angle PML+\angle NPM=\angle PML+\angle RPM=90^{\circ}$，
故 $\angle KPN=\angle PML$．因此
$
\dfrac{\frac{T N}{2}}{r}=\sin \angle K P N=\sin \angle P M L=\dfrac{\frac{r}{2}}{x}
$
从而 $TN=\dfrac{r^2}{x}=OT$，即以 $T$ 为圆心，$TN$ 为半径的圆过点 $O$．
答案
解析
备注
