在所示的图形中,方格 $P$ 的左右两侧分别有 $a$ 个和 $b$ 个方格,上下两侧分别有 $c$ 个和 $d$ 个方格,$a,b,c,d$ 为正整数,满足 $(a-b)(c-d)=0$.称由这些方格所组成的图形为一个"十字星".现有一张由 $2014$ 个方格所组成的 $38\times 53$ 矩形方格表,求该方格表中十字星的个数.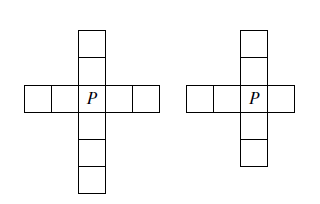
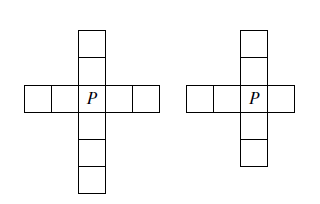
【难度】
【出处】
2014中国东南数学奥林匹克试题(高二)
【标注】
【答案】
略
【解析】
对于一个十字星,将题目中所指的方格 $P$ 称为该十字星的"中心块",当 $a=b$ 时,称该十字星为"站着的";当 $c=d$ 时,称其为"躺着的"(有些十字星既是站着的又是躺着的).
若一个矩形 $R$ 的一行一列的并集刚好是某个十字星 $S$,则称 $R$ 是 $S$ 的"源矩形.在源矩形 $R$ 中,十字星 $S$ 由中心块的位置唯一确定,且不同的源矩形对应的十字星必不相同.此外由十字星的定义知,源矩形的行数与列数至少是3;行数为偶数的源矩形不会躺着的十字星;列数为偶效的源矩形不含站着的十字星.
现若虑 $m$ 行 $n$ 列的矩形方格表 $P_{m,n}$.用 $A,B,C$ 分别表示 $P_{m,n}$ 中躺着的十字星,站着的十子星,既站着又躺着的十字星的个数.
在 $P_{m,n}$ 中,$2k+1$ 行列的源矩形的个数为 $(m-2k)(n-l+1)$,其中 $k,l$ 满足 $3\leqslant 2k+1\leqslant m$,$3\leqslant l\leqslant n$.对每个 $2k+1$ 行 $l$ 列的源矩形,躺着的十字星的中心块必在第 $k+1$ 行,且位于第 $2$ 至 $l-1$ 列,故此源矩形对应 $l-2$ 个躺着的十字星.所以
$\begin{aligned} A &=\sum_{k=1}^{\left[\frac{m-1}{2}\right]} \sum_{l=3}^{n}(l-2)(m-2 k)(n-l+1) \\ &=\sum_{k=1}^{\left[\frac{m-1}{2}\right]}(m-2 k) \cdot \sum_{l=1}^{n-2} l(n-l-1) \end{aligned}$
其中
$\begin{aligned} \sum_{k=1}^{\left[\frac{m-1}{2}\right]}(m-2 k) &=\left[\frac{m-1}{2}\right] \cdot \frac{(m-2)+\left(m-2\left[\frac{m-1}{2}\right]\right)}{2} \\ &=\left[\frac{m-1}{2}\right]\left(m-\left[\frac{m+1}{2}\right]\right) \\ \sum_{l=1}^{n-2} l(n-l-1) &=\left(\sum_{l=1}^{n-2} l\right)(n-1)-\sum_{l=1}^{n-2} l^{2} \\ &=\frac{(n-2)(n-1)^{2}}{2}-\frac{(n-2)(n-1)(2 n-3)}{6} \\ &=\frac{n(n-1)(n-2)}{6} \end{aligned}$
所以 $A=\left[\dfrac{m-1}{2}\right]\left(m-\left[\dfrac{m+1}{2}\right]\right) \cdot \dfrac{n(n-1)(n-2)}{6}$ ①
同理,$P_{m,n}$ 所含的 $k$ 行 $2l+1$ 列的源矩形的个数为 $(m-k+1)(n-2l)$,每个 $k$ 行 $2l+1$ 列时源矩形对应 $k-2$ 个站着的十字星,进而
$\begin{aligned} B &=\sum_{k=3}^{m} \sum_{l=1}^{\left[\frac{n-1}{2}\right]}(k-2)(m-k+1)(n-2 l) \\ &=\left[\frac{n-1}{2}\right]\left(n-\left[\frac{n+1}{2}\right]\right) \cdot \frac{m(m-1)(m-2)}{6} \end{aligned}$
每个 $2k+1$ 行 $2l+1$ 列的源矩形恰对应一个既站着又躺着的十字星(中心块位于源矩形的中心),而 $P_{m,n}$ 中含有 $(m-2k)(n-2l)$ 个这样的源矩形,故类似得到
$\begin{aligned} C &=\sum_{k=1}^{\left[\frac{m-1}{2}\right]}\sum_{l=1}^{\left[\frac{n-1}{2}\right]}(m-2 k)(n-2 l) \\ &=\left[\frac{m-1}{2}\right]\left(m-\left[\frac{m+1}{2}\right]\right)\left[\frac{n-1}{2}\right]\left(n-\left[\frac{n+1}{2}\right]\right) \end{aligned}$ ③
这正是在 $A+B$ 中被重复计数的十字星个数.
特别地,对 $m=38,n=53$ 的情形,有
$\begin{aligned}\left[\frac{m-1}{2}\right]\left(m-\left[\frac{m+1}{2}\right]\right) &=18 \times 19=342 \\ \frac{m(m-1)(m-2)}{6} &=8436 \\\left[\frac{n-1}{2}\right]\left(n-\left[\frac{n+1}{2}\right]\right) &=26 \times 26=676 \\ \frac{n(n-1)(n-2)}{6} &=23426 \end{aligned}$
代入 ①,②,③ 得
$\begin{array}{l}{A=342 \times 23426=8011692} \\ {B=676 \times 8436=5702736} \\ {C=342 \times 676=231192}\end{array}$
从而,方格表 $P_{38,53}$ 含有的十字星个数为 $A+B-C=13483236$.
若一个矩形 $R$ 的一行一列的并集刚好是某个十字星 $S$,则称 $R$ 是 $S$ 的"源矩形.在源矩形 $R$ 中,十字星 $S$ 由中心块的位置唯一确定,且不同的源矩形对应的十字星必不相同.此外由十字星的定义知,源矩形的行数与列数至少是3;行数为偶数的源矩形不会躺着的十字星;列数为偶效的源矩形不含站着的十字星.
现若虑 $m$ 行 $n$ 列的矩形方格表 $P_{m,n}$.用 $A,B,C$ 分别表示 $P_{m,n}$ 中躺着的十字星,站着的十子星,既站着又躺着的十字星的个数.
在 $P_{m,n}$ 中,$2k+1$ 行列的源矩形的个数为 $(m-2k)(n-l+1)$,其中 $k,l$ 满足 $3\leqslant 2k+1\leqslant m$,$3\leqslant l\leqslant n$.对每个 $2k+1$ 行 $l$ 列的源矩形,躺着的十字星的中心块必在第 $k+1$ 行,且位于第 $2$ 至 $l-1$ 列,故此源矩形对应 $l-2$ 个躺着的十字星.所以
$\begin{aligned} A &=\sum_{k=1}^{\left[\frac{m-1}{2}\right]} \sum_{l=3}^{n}(l-2)(m-2 k)(n-l+1) \\ &=\sum_{k=1}^{\left[\frac{m-1}{2}\right]}(m-2 k) \cdot \sum_{l=1}^{n-2} l(n-l-1) \end{aligned}$
其中
$\begin{aligned} \sum_{k=1}^{\left[\frac{m-1}{2}\right]}(m-2 k) &=\left[\frac{m-1}{2}\right] \cdot \frac{(m-2)+\left(m-2\left[\frac{m-1}{2}\right]\right)}{2} \\ &=\left[\frac{m-1}{2}\right]\left(m-\left[\frac{m+1}{2}\right]\right) \\ \sum_{l=1}^{n-2} l(n-l-1) &=\left(\sum_{l=1}^{n-2} l\right)(n-1)-\sum_{l=1}^{n-2} l^{2} \\ &=\frac{(n-2)(n-1)^{2}}{2}-\frac{(n-2)(n-1)(2 n-3)}{6} \\ &=\frac{n(n-1)(n-2)}{6} \end{aligned}$
所以 $A=\left[\dfrac{m-1}{2}\right]\left(m-\left[\dfrac{m+1}{2}\right]\right) \cdot \dfrac{n(n-1)(n-2)}{6}$ ①
同理,$P_{m,n}$ 所含的 $k$ 行 $2l+1$ 列的源矩形的个数为 $(m-k+1)(n-2l)$,每个 $k$ 行 $2l+1$ 列时源矩形对应 $k-2$ 个站着的十字星,进而
$\begin{aligned} B &=\sum_{k=3}^{m} \sum_{l=1}^{\left[\frac{n-1}{2}\right]}(k-2)(m-k+1)(n-2 l) \\ &=\left[\frac{n-1}{2}\right]\left(n-\left[\frac{n+1}{2}\right]\right) \cdot \frac{m(m-1)(m-2)}{6} \end{aligned}$
每个 $2k+1$ 行 $2l+1$ 列的源矩形恰对应一个既站着又躺着的十字星(中心块位于源矩形的中心),而 $P_{m,n}$ 中含有 $(m-2k)(n-2l)$ 个这样的源矩形,故类似得到
$\begin{aligned} C &=\sum_{k=1}^{\left[\frac{m-1}{2}\right]}\sum_{l=1}^{\left[\frac{n-1}{2}\right]}(m-2 k)(n-2 l) \\ &=\left[\frac{m-1}{2}\right]\left(m-\left[\frac{m+1}{2}\right]\right)\left[\frac{n-1}{2}\right]\left(n-\left[\frac{n+1}{2}\right]\right) \end{aligned}$ ③
这正是在 $A+B$ 中被重复计数的十字星个数.
特别地,对 $m=38,n=53$ 的情形,有
$\begin{aligned}\left[\frac{m-1}{2}\right]\left(m-\left[\frac{m+1}{2}\right]\right) &=18 \times 19=342 \\ \frac{m(m-1)(m-2)}{6} &=8436 \\\left[\frac{n-1}{2}\right]\left(n-\left[\frac{n+1}{2}\right]\right) &=26 \times 26=676 \\ \frac{n(n-1)(n-2)}{6} &=23426 \end{aligned}$
代入 ①,②,③ 得
$\begin{array}{l}{A=342 \times 23426=8011692} \\ {B=676 \times 8436=5702736} \\ {C=342 \times 676=231192}\end{array}$
从而,方格表 $P_{38,53}$ 含有的十字星个数为 $A+B-C=13483236$.
答案
解析
备注