如图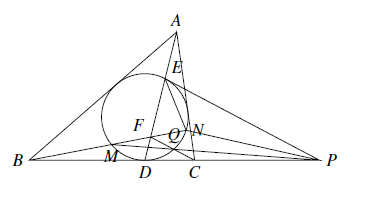
在 $\triangle ABC$ 中，$AB>AC$，内切圆 $I$ 与 $BC$ 边切于点 $D$，$AD$ 交内切圆 $I$ 于另一点 $E$，圆 $I$ 的切线 $EP$ 交 $BC$ 的延长线于点 $P$，$CF$ 平行 $PE$ 交 $AD$ 于点 $F$，直线 $BF$ 交圆 $I$ 于点 $M,N$，点 $M$ 在线段 $BF$ 上，线段 $PM$ 与圆 $I$ 交于另一点 $Q$．证明：$\angle ENP=\angle ENQ$．
在 $\triangle ABC$ 中，$AB>AC$，内切圆 $I$ 与 $BC$ 边切于点 $D$，$AD$ 交内切圆 $I$ 于另一点 $E$，圆 $I$ 的切线 $EP$ 交 $BC$ 的延长线于点 $P$，$CF$ 平行 $PE$ 交 $AD$ 于点 $F$，直线 $BF$ 交圆 $I$ 于点 $M,N$，点 $M$ 在线段 $BF$ 上，线段 $PM$ 与圆 $I$ 交于另一点 $Q$．证明：$\angle ENP=\angle ENQ$．【难度】
【出处】
2013中国东南数学奥林匹克试题
【标注】
【答案】
略
【解析】
证法一
设圆 $I$ 与 $AC,AB$ 分别切于点 $S,T$，连结 $ST, AI, IT$，设 $ST$ 与 $AI$ 交于点 $G$，则 $IT\perp AT, TG\perp AI$，从而有 $AG\cdot AI=AT^2 =AD\cdot AE$，所以 $I,G,E,D$ 四点共圆．又 $IE\perp PE,ID\perp PD$，所以 $I,E,P,D$ 四点共圆，从而 $I,G,E,P,D$ 五点共圆．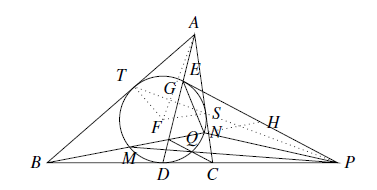
所以 $\angle IGP=\angle IEP=90^{\circ}$，即 $IG\perp PG$，
从而 $P,S,T$ 三点共线．
直线 $PST$ 截 $\triangle ABC$，由梅涅劳斯定理知，
$
\dfrac{A S}{S C} \cdot \dfrac{C P}{P B} \cdot \dfrac{B T}{T A}=1
$
又 $AS=AT,CS=CD,BT=BD$，所以有
$\dfrac{P C}{P B} \cdot \dfrac{B D}{C D}=1
$ ①
设 $BN$ 的延长线交 $PE$ 于点 $H$，直线 $BFH$ 截 $\triangle PDE$，由梅涅劳斯定理知，
$
\dfrac{P H}{H E} \cdot \dfrac{E F}{F D} \cdot \dfrac{D B}{B P}=1
$
因为 $CF$ 平行于 $BE$，所以 $\dfrac{EF}{FD}=\dfrac{PC}{CD}$，从而有
$\dfrac{P H}{H E} \cdot \dfrac{P C}{C D} \cdot \dfrac{D B}{B P}=1$ ②
由 ①，② 知，$PH=HE$，故 $PH^2 =HE^2 =HM\cdot HN$，所以 $\frac{PH}{HM}=\frac{HN}{PH}$，$\triangle PHN\sim\triangle MHP$，$\angle HPN=\angle HMP=\angle NEQ$，又 $\angle PEN=\angle EQN$，
所以 $\angle ENP=\angle ENQ$．
证法二
设圆 $I$ 与 $AC,AB$ 分别切于点 $S,T$，则由 $PI\perp AD$ 知
$
P A^{2}-P D^{2}=I A^{2}-I D^{2}=I A^{2}-I T^{2}=A T^{2}
$
所以 $PA^2 - AT^2 = PD^2 = IP^2 - ID^2 = IP^2 - IT^2$，从而 $AI\perp PT$．又 $AI\perp ST$，所以 $P,S,T$ 三点共线．
以下同证法一．
设圆 $I$ 与 $AC,AB$ 分别切于点 $S,T$，连结 $ST, AI, IT$，设 $ST$ 与 $AI$ 交于点 $G$，则 $IT\perp AT, TG\perp AI$，从而有 $AG\cdot AI=AT^2 =AD\cdot AE$，所以 $I,G,E,D$ 四点共圆．又 $IE\perp PE,ID\perp PD$，所以 $I,E,P,D$ 四点共圆，从而 $I,G,E,P,D$ 五点共圆．
所以 $\angle IGP=\angle IEP=90^{\circ}$，即 $IG\perp PG$，从而 $P,S,T$ 三点共线．
直线 $PST$ 截 $\triangle ABC$，由梅涅劳斯定理知，
$
\dfrac{A S}{S C} \cdot \dfrac{C P}{P B} \cdot \dfrac{B T}{T A}=1
$
又 $AS=AT,CS=CD,BT=BD$，所以有
$\dfrac{P C}{P B} \cdot \dfrac{B D}{C D}=1
$ ①
设 $BN$ 的延长线交 $PE$ 于点 $H$，直线 $BFH$ 截 $\triangle PDE$，由梅涅劳斯定理知，
$
\dfrac{P H}{H E} \cdot \dfrac{E F}{F D} \cdot \dfrac{D B}{B P}=1
$
因为 $CF$ 平行于 $BE$，所以 $\dfrac{EF}{FD}=\dfrac{PC}{CD}$，从而有
$\dfrac{P H}{H E} \cdot \dfrac{P C}{C D} \cdot \dfrac{D B}{B P}=1$ ②
由 ①，② 知，$PH=HE$，故 $PH^2 =HE^2 =HM\cdot HN$，所以 $\frac{PH}{HM}=\frac{HN}{PH}$，$\triangle PHN\sim\triangle MHP$，$\angle HPN=\angle HMP=\angle NEQ$，又 $\angle PEN=\angle EQN$，
所以 $\angle ENP=\angle ENQ$．
证法二
设圆 $I$ 与 $AC,AB$ 分别切于点 $S,T$，则由 $PI\perp AD$ 知
$
P A^{2}-P D^{2}=I A^{2}-I D^{2}=I A^{2}-I T^{2}=A T^{2}
$
所以 $PA^2 - AT^2 = PD^2 = IP^2 - ID^2 = IP^2 - IT^2$，从而 $AI\perp PT$．又 $AI\perp ST$，所以 $P,S,T$ 三点共线．
以下同证法一．
答案
解析
备注
