十二个杂技演员编号分别为 $1,2,\ldots,12$，将他们按适当方式分别围成 $A,B$ 两个圈，每圈 $6$ 人，其中 $B$ 圈的每个演员分别站在 $A$ 圈相邻两个演员的肩膀上．如果 $B$ 圈中每个演员的编号分别等于他脚下两个演员的编号之和，就称这样搭配成的结构为一个"塔"，问总共能搭配成多少个结构不相同的"塔"？
（注：旋转或对称后的塔属于同一种结构．以 $8$ 个人的情况为例，画一个圆，将底层演员编号填在圈内，上层演员编号填在圈外，那么以下三个图均是"塔"，但后两个图分别可由第一个图经旋转或对称而得，故它们属于同一种结构．）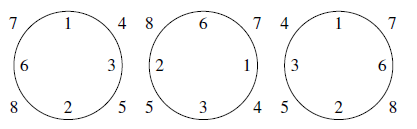
（注：旋转或对称后的塔属于同一种结构．以 $8$ 个人的情况为例，画一个圆，将底层演员编号填在圈内，上层演员编号填在圈外，那么以下三个图均是"塔"，但后两个图分别可由第一个图经旋转或对称而得，故它们属于同一种结构．）
【难度】
【出处】
2013中国东南数学奥林匹克试题
【标注】
【答案】
略
【解析】
将组 $A,B$ 中的元素和分别记为 $x,y$，则有 $y=2x$，所以 $
3 x=x+y=1+2+\ldots+12=78, ~~~~x=26
$．
显然有 $1,2\in A$，$11,12\in B$，设 $A=\{1,2,a,b,c,d\}$，其中 $a<b<c<d$，则 $a+b+c+d=23$，且 $a\geqslant 3,8\leqslant d\leqslant 10$（若 $d\leqslant 7$，则 $a+b+c+d\leqslant 4+5+6+7=22$，矛盾）．
（1）如果 $d=8$，则 $A=\{1,2,a,b,c,8\}$，$c\leqslant 7$，$a+b+c=15$，于是 $(a,b,c)=(3,5,7)$ 或 $(4,5,6)$，即 $A=\{1,2,3,5,7,8\}$ 或 $A=\{1,2,4,5,6,8\}$．
若 $A=\{1,2,3,5,7,8\}$，则 $B=\{4,6,9,10,11,12\}$，由于 $B$ 中含 $4,6,11,12$，故 $A$ 中须 $1,3$ 邻接，$1,5$ 邻接，$5,7$ 邻接，$8,3$ 邻接，这时只有唯一的排法，由此得到一个塔．
若 $A=\{1,2,4,5,6,8\}$，则 $B=\{3,7,9,10,11,12\}$，类似知 $A$ 中必须 $1,2$ 邻接，$5,6$ 邻接，$4,8$ 邻接，这时有两种排法，得到两个塔．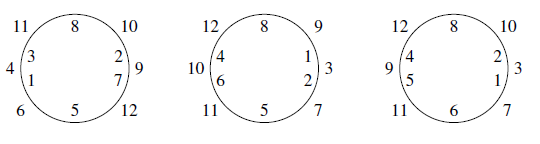
（2）如果 $d=9$，则 $A=\{1,2,a,b,c,9\},c\leqslant 8,a+b+c=14$，这时 $(a,b,c)=(3,5,6)$ 或 $(3,4,7)$，即 $A=\{1,2,3,5,6,9\}$ 或 $A=\{1,2,3,4,7,9\}$．
若 $A=\{1,2,3,4,7,9\}$，则 $B=\{4,7,8,10,11,12\}$，为得到 $B$ 中的 $4,10,12$，$A$ 中必须 $1,3,9$ 两两邻接，这不可能．
若 $A=\{1,2,3,4,7,9\}$，则 $B=\{5,6,8,10,11,12\}$，为得到 $B$ 中的 $6,8,12$，$A$ 中必须 $2,4$ 邻接，$1,7$ 邻接，$9,3$ 邻接，于是有两种排法，得到两个塔．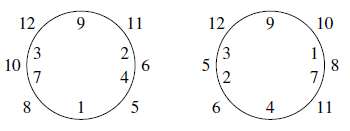
（3）如果 $d=10$，则 $A=\{1,2,a,b,c,10\}, c\leqslant 9,a+b+c=13$，这时，$(a,b,c)=(3,4,6)$ 即 $A=\{1,2,3,4,6,10\}$，$B=\{5,7,8,9,11,12\}$，为得到 $B$ 中 $8,9,11,12$，$A$ 中必须 $6,2$ 邻接，$6,3$ 邻接，$10,1$ 邻接，$10,2$ 邻接，只有唯一排法，得到一个塔．
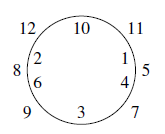因此，结构不相同的"塔"共有6个．
3 x=x+y=1+2+\ldots+12=78, ~~~~x=26
$．
显然有 $1,2\in A$，$11,12\in B$，设 $A=\{1,2,a,b,c,d\}$，其中 $a<b<c<d$，则 $a+b+c+d=23$，且 $a\geqslant 3,8\leqslant d\leqslant 10$（若 $d\leqslant 7$，则 $a+b+c+d\leqslant 4+5+6+7=22$，矛盾）．
（1）如果 $d=8$，则 $A=\{1,2,a,b,c,8\}$，$c\leqslant 7$，$a+b+c=15$，于是 $(a,b,c)=(3,5,7)$ 或 $(4,5,6)$，即 $A=\{1,2,3,5,7,8\}$ 或 $A=\{1,2,4,5,6,8\}$．
若 $A=\{1,2,3,5,7,8\}$，则 $B=\{4,6,9,10,11,12\}$，由于 $B$ 中含 $4,6,11,12$，故 $A$ 中须 $1,3$ 邻接，$1,5$ 邻接，$5,7$ 邻接，$8,3$ 邻接，这时只有唯一的排法，由此得到一个塔．
若 $A=\{1,2,4,5,6,8\}$，则 $B=\{3,7,9,10,11,12\}$，类似知 $A$ 中必须 $1,2$ 邻接，$5,6$ 邻接，$4,8$ 邻接，这时有两种排法，得到两个塔．
（2）如果 $d=9$，则 $A=\{1,2,a,b,c,9\},c\leqslant 8,a+b+c=14$，这时 $(a,b,c)=(3,5,6)$ 或 $(3,4,7)$，即 $A=\{1,2,3,5,6,9\}$ 或 $A=\{1,2,3,4,7,9\}$．若 $A=\{1,2,3,4,7,9\}$，则 $B=\{4,7,8,10,11,12\}$，为得到 $B$ 中的 $4,10,12$，$A$ 中必须 $1,3,9$ 两两邻接，这不可能．
若 $A=\{1,2,3,4,7,9\}$，则 $B=\{5,6,8,10,11,12\}$，为得到 $B$ 中的 $6,8,12$，$A$ 中必须 $2,4$ 邻接，$1,7$ 邻接，$9,3$ 邻接，于是有两种排法，得到两个塔．
（3）如果 $d=10$，则 $A=\{1,2,a,b,c,10\}, c\leqslant 9,a+b+c=13$，这时，$(a,b,c)=(3,4,6)$ 即 $A=\{1,2,3,4,6,10\}$，$B=\{5,7,8,9,11,12\}$，为得到 $B$ 中 $8,9,11,12$，$A$ 中必须 $6,2$ 邻接，$6,3$ 邻接，$10,1$ 邻接，$10,2$ 邻接，只有唯一排法，得到一个塔．因此，结构不相同的"塔"共有6个．
答案
解析
备注
