将 $3\times 3$ 正方形任意一个用上的 $2\times 2$ 正方形挖去，剩下的图形称为"角形"（例如，下图就是一个角形）．
现于 $10\times 10$ 方格表中放置一些两两不重叠的角形，要求角形的边界与方格表的边界或分格线重合．求正整数 $k$ 的最大值，使得无论以何种方式放置了 $k$ 个角形之后，总能在方格表中再放入一个完整的角形．
现于 $10\times 10$ 方格表中放置一些两两不重叠的角形，要求角形的边界与方格表的边界或分格线重合．求正整数 $k$ 的最大值，使得无论以何种方式放置了 $k$ 个角形之后，总能在方格表中再放入一个完整的角形．【难度】
【出处】
2013中国东南数学奥林匹克试题
【标注】
【答案】
略
【解析】
首先有 $k_{\max}< 8$，这是因为，若按下图的方式放置 $8$ 个角形，则不能再于方格表中放入另一个角形．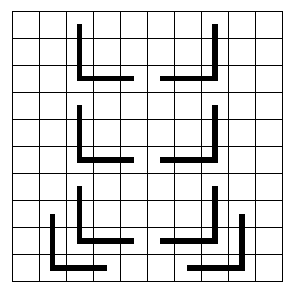
下面证明：任意放置 $7$ 个角形后，仍可再放人一个完整的角形．
将 $10\times 10$ 方格表的第 $5,6$ 行及第 $5,6$ 列遮住，留出 $4$ 个 $4\times 4$ 正方形．当放置 $7$ 个角形后，由于每个角形不能与两个上述 $4\times 4$ 正方形相交，故根据抽屉原理知，必存在一个 $4\times 4$ 的正方形 $S$，使得与 $S$ 相交的角形至多 $1$ 个，而角形可被 $3\times 3$ 正万形所包含，故正方形 $S$ 被角形所占据的部分必包含于它的某个角上的 $3\times 3$ 正方形．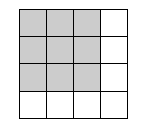
如图所示，我们可以在 $S$ 除去一个角上 $3\times 3$ 正方形后剩余的部分放置一个新的角形．因此 $k=7$ 时符合题意．
综上所述，有 $k_{\max}=7$．
下面证明：任意放置 $7$ 个角形后，仍可再放人一个完整的角形．将 $10\times 10$ 方格表的第 $5,6$ 行及第 $5,6$ 列遮住，留出 $4$ 个 $4\times 4$ 正方形．当放置 $7$ 个角形后，由于每个角形不能与两个上述 $4\times 4$ 正方形相交，故根据抽屉原理知，必存在一个 $4\times 4$ 的正方形 $S$，使得与 $S$ 相交的角形至多 $1$ 个，而角形可被 $3\times 3$ 正万形所包含，故正方形 $S$ 被角形所占据的部分必包含于它的某个角上的 $3\times 3$ 正方形．
如图所示，我们可以在 $S$ 除去一个角上 $3\times 3$ 正方形后剩余的部分放置一个新的角形．因此 $k=7$ 时符合题意．综上所述，有 $k_{\max}=7$．
答案
解析
备注
