如图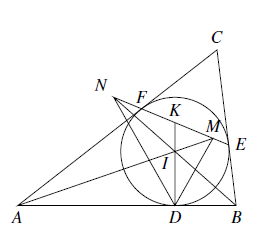
$\triangle ABC$ 的内切圆 $I$ 在边 $AB,BC,CA$ 上的切点分别是 $D,E,F$，直线 $EF$ 与直线 $AI,BI,DI$ 分别相交于点 $M,N,K$．证明：$DM\cdot KE=DN\cdot KF$．
$\triangle ABC$ 的内切圆 $I$ 在边 $AB,BC,CA$ 上的切点分别是 $D,E,F$，直线 $EF$ 与直线 $AI,BI,DI$ 分别相交于点 $M,N,K$．证明：$DM\cdot KE=DN\cdot KF$．【难度】
【出处】
2012中国东南数学奥林匹克试题
【标注】
【答案】
略
【解析】
易知 $I,D,E,B$ 四点共圆．又 $\angle A I D=90^{\circ}-\angle I A D$，$\angle M E D=\angle F D A=90^{\circ}-\angle I A D$，所以 $\angle AID=\angle MED$，于是 $I,D,E,M$ 四点共圆．
从而 $I,D,B,E,M$ 五点共圆，$\angle IMB=\angle IEB=90^{\circ}$，即 $AM \perp BM$．
同理，$I,D,A,N,F$ 五点共圆，且 $BN\perp AN$．
设直线 $AN,BM$ 交于点 $G$（如图），则易知点 $I$ 为 $\triangle GAB$ 的垂心．又 $ID\perp AB$，所以 $G,I,D$ 共线．由 $G,N,D,B$ 四点共圆，知 $\angle ADN=\angle G$．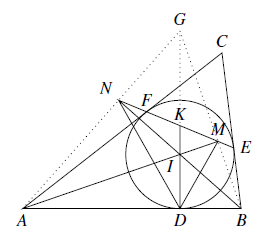
同理 $\angle BDM=\angle G$．所以 $DK$ 平分 $\angle MDN$，从而 $
\dfrac{D M}{D N}=\dfrac{K M}{K N}
$ ①
又由 $I,D,E,M$；$I,D,N,F$ 分别共圆，知 $KM\cdot KE=KI\cdot KD=KF\cdot KN$
所以 $\dfrac{KM}{KN}=\dfrac{KF}{KE}
$ ②
由 ①，② 知 $\dfrac{D M}{D N}=\dfrac{K F}{K E}$，即 $D M \cdot K E=D N \cdot K F$．
从而 $I,D,B,E,M$ 五点共圆，$\angle IMB=\angle IEB=90^{\circ}$，即 $AM \perp BM$．
同理，$I,D,A,N,F$ 五点共圆，且 $BN\perp AN$．
设直线 $AN,BM$ 交于点 $G$（如图），则易知点 $I$ 为 $\triangle GAB$ 的垂心．又 $ID\perp AB$，所以 $G,I,D$ 共线．由 $G,N,D,B$ 四点共圆，知 $\angle ADN=\angle G$．
同理 $\angle BDM=\angle G$．所以 $DK$ 平分 $\angle MDN$，从而 $\dfrac{D M}{D N}=\dfrac{K M}{K N}
$ ①
又由 $I,D,E,M$；$I,D,N,F$ 分别共圆，知 $KM\cdot KE=KI\cdot KD=KF\cdot KN$
所以 $\dfrac{KM}{KN}=\dfrac{KF}{KE}
$ ②
由 ①，② 知 $\dfrac{D M}{D N}=\dfrac{K F}{K E}$，即 $D M \cdot K E=D N \cdot K F$．
答案
解析
备注
