查看数据源：5d4a422a210b280220ed754a
如图$\triangle ABC$ 中，$D$ 为边 $AC$ 上一点且 $\angle ABD=\angle C$，点 $E$ 在边 $AB$ 上且 $BE=DE$，设 $M$ 为 $CD$ 中点，$AH\perp DE$ 于点 $H$．已知 $AH=2-\sqrt{3}$，$AB=1$，求 $\angle AME$ 的度数．
【难度】
【出处】
2012中国东南数学奥林匹克试题
【标注】
  • 知识点
    >
    二试几何部分
【答案】
略
【解析】
证法一
由已知，$\triangle BCD$ 的外接圆 $O$ 与直线 $AB$ 切于点 $B$．作 $AN\perp BD$ 于点 $N$，$EG\parallel BD$ 交 $AC$ 于点 $G$．连结 $OB,OE,OG,OD,OM$，如图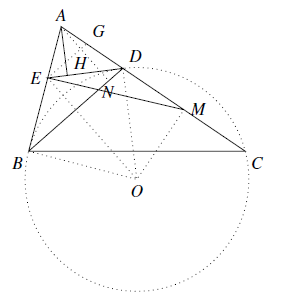．又显然 $OE\perp BD$，$OM\perp CD$，所以 $\angle GEO=90^{\circ}=\angle GMO$，则 $E,G,M,O$ 四点共圆，从而
$
\tan \angle A M E=\tan \angle G O E=\dfrac{E G}{O E}
$
由 $\angle OBE=\angle BNA=90^{\circ}$，$\angle ABN=\angle C=\angle EOB$ 知：$\triangle OBE$ 与 $\triangle BNA$ 相似．
易知 $A,H,N,D$ 四点共圆，故 $\angle EDG=\angle ANH$，又
$\angle AHN=180^{\circ}-\angle ADN=\angle EGD$
故 $\triangle EGD$ 与 $\triangle AHN$ 相似．所以 $
\dfrac{O E}{B A}=\dfrac{B E}{N A}=\dfrac{D E}{N A}=\dfrac{E G}{A H}
$
于是 $\dfrac{E G}{O E}=\dfrac{A H}{A B}=2-\sqrt{3}$，从而 $\angle AME=15^{\circ}$．
证法二
设 $\angle ABD=\angle C=\alpha$，$\angle DBC=\beta$，由已知易得
$\begin{array}{c}{\angle B D E=\alpha, \angle A E D=2 \alpha} \\ {\angle A D E=\angle A D B-\angle B D E=(\alpha+\beta)-\alpha=\beta} \\ {A B=A E+E B=A E+E H+H D}\end{array}$
因此 $\dfrac{A B}{A H}=\dfrac{A E+E H}{A H}+\dfrac{H D}{A H}=\dfrac{1+\cos 2 \alpha}{\sin 2 \alpha}+\cot \beta=\cot \alpha+\cot \beta
$ ①
作 $EK\perp AC$，$EL\perp BD$，垂足为 $K,L$（如图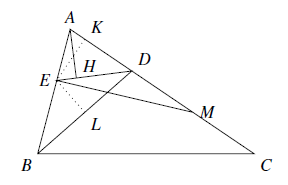）则 $L$ 为 $BD$ 中点，结合正弦定理得
$
\dfrac{E L}{E K} =\dfrac{D E \sin \angle E D L}{D E \sin \angle E D K}=\dfrac{\sin \alpha}{\sin \beta} =\dfrac{B D}{C D}=\dfrac{L D}{M D}
$
所以 $\cot \alpha=\dfrac{L D}{E L}=\dfrac{M D}{E K}=\dfrac{M K}{E K}-\dfrac{D K}{E K}=\cot \angle A M E-\cot \beta$ ②
由 ①，② 及已知条件得
$
\cot \angle A M E=\dfrac{A B}{A H}=\dfrac{1}{2-\sqrt{3}}=2+\sqrt{3}
$
从而 $\angle AME=15^{\circ}$．
答案 解析 备注
0.186629s