过 $\triangle ABC$ 的外心 $O$ 任作一直线，分别交边 $AB、AC$ 于 $M,N$，$E,F$ 分别是 $BN、CM$ 的中点．证明：$\angle EOF=\angle A$．
【难度】
【出处】
2011中国东南数学奥林匹克试题
【标注】
【答案】
略
【解析】
我们证明结论对任何三角形都成立．
分三种情况考虑，对于直角三角形 $ABC$，结论是显然的，事实 上．如图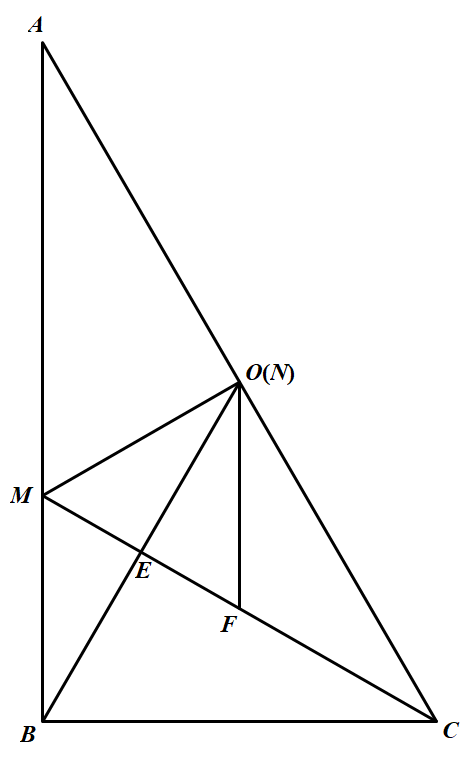
若 $\angle ABC$ 为直角，则外心 $O$ 是斜边 $AC$ 的中点，过 $O$ 的直线交 $AB、AC$ 于 $M、N$，则 $O、N$ 共点，由于 $F$ 是 $CM$ 的中 点．故中位线 $OF\parallel AM$，所以 $\angle EOF=\angle OBA=\angle OAB=\angle A$；
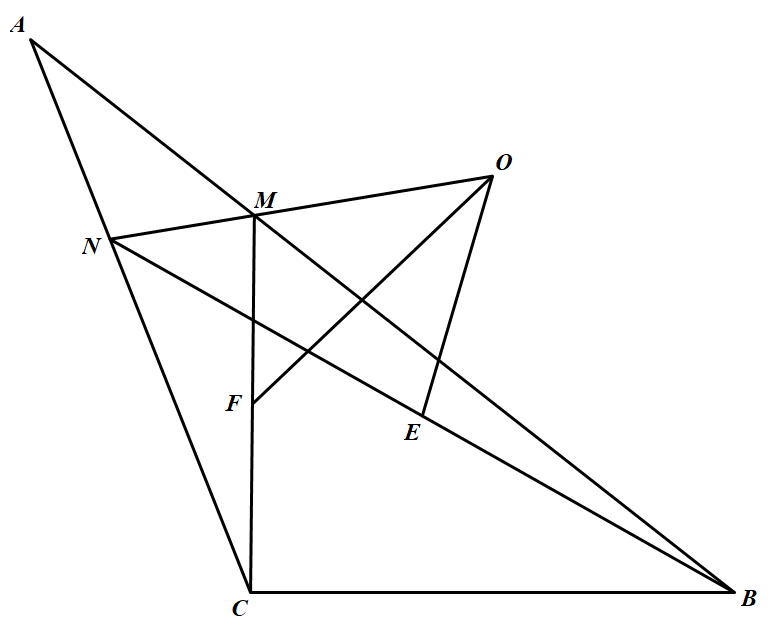
以下考虑 $\triangle ABC$ 为锐角三角形或钝角三角形的情况（如下图）．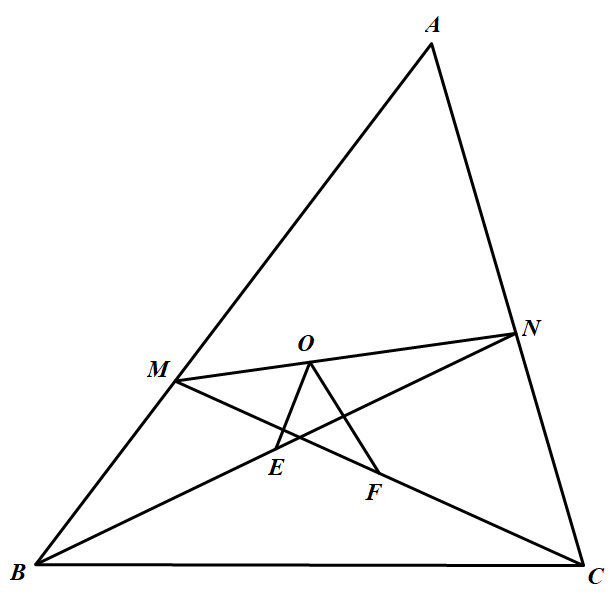
先证引理：如图，过 $\odot O$ 的直径 $KL$ 上的两点 $A,B$ 分别作弦 $CD,EF$，连结 $CE,DF$，分别交 $KL$ 于 $M,N$，若 $OA=OB$，则 $MA=NB$．
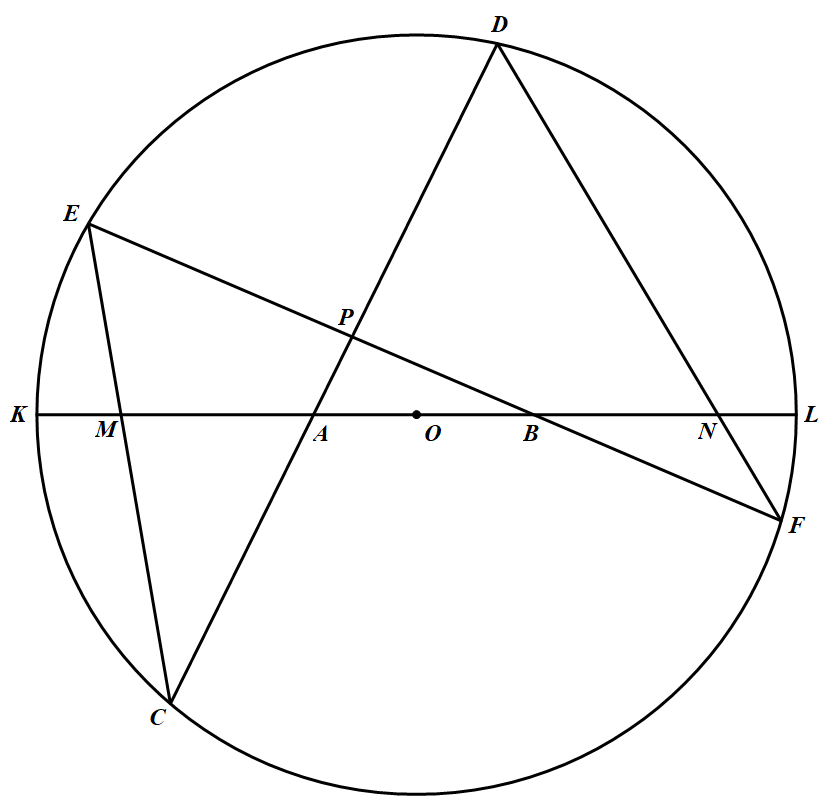引理证明：设 $CD $ 交 $EF$ 于点 $ P$，直线 $CE、DF$ 分别截 $\triangle PAB$，据梅涅劳斯定理，$\dfrac{A C}{C P} \cdot \dfrac{P E}{E B} \cdot \dfrac{B M}{M A}=1,\dfrac{B F}{F P} \cdot \dfrac{P D}{D A} \cdot \dfrac{A N}{N B}=1$；
则 $\dfrac{M A}{N B}=\dfrac{A C \cdot A D \cdot P E \cdot P F \cdot B M}{B E \cdot B F \cdot P C \cdot P D \cdot A N}$ ①
而由相交弦，得 $P C \cdot P D=P E \cdot P F$ ②
若 $\odot O$ 的半径为 $R,QA= OB= a$，则 $A C \cdot A D=A K \cdot A L=R^{2}-a^{2}=B K \cdot B L=B E \cdot B F$ ③
据 ①②③ 得，$\dfrac{M A}{N B}=\dfrac{M B}{N A}$，即 $\dfrac{M A}{N B}=\dfrac{M A+A B}{N B+A B}=\dfrac{A B}{A B}=1$．
因此 $MA=NB$．引理得证．
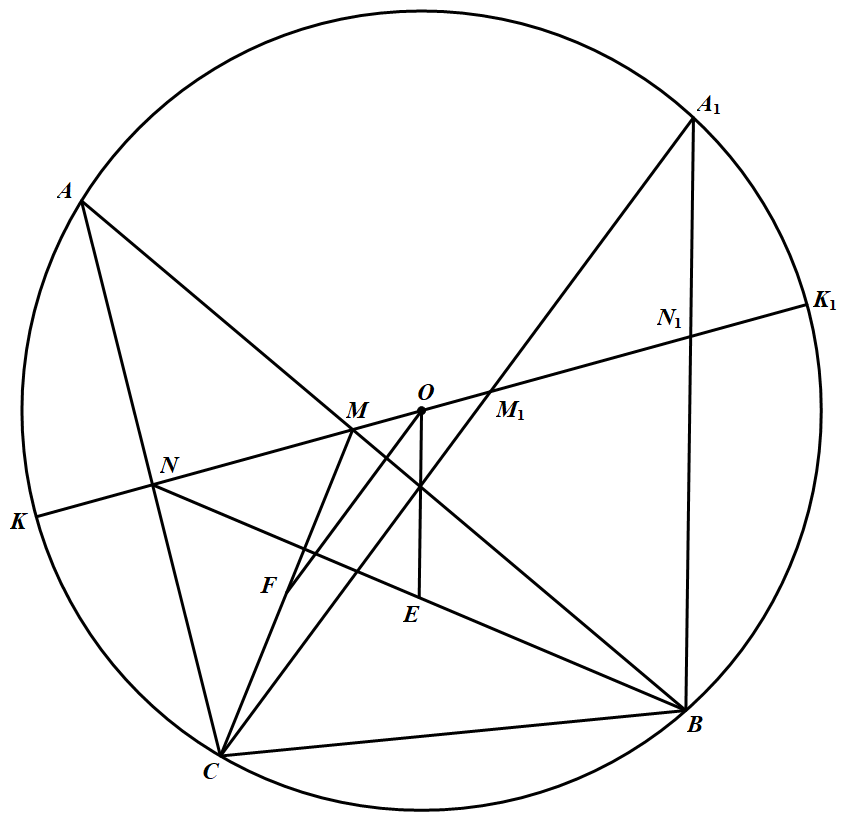
回到本题，如下图（两图都适用），延长 $MN$ 得直径 $KK_1$，在直径上取点 $M_1$，使 $OM_1=OM$，设 $CM_1\bigcap \odot O=A_1$，连 $A_1B$ 交 $KK_1$ 于 $N_1$．由引理，$MN_1= M_1N$（下二图中则是 $M_1N_1=MN$）．因此，$O$ 是 $NN_1$ 的中点，故 $OE、OF$ 分别是 $\triangle NBN_1$ 及 $\triangle MCM_1$ 的中位线，于是得 $\angle EOF=\angle BA_1C=\angle A$．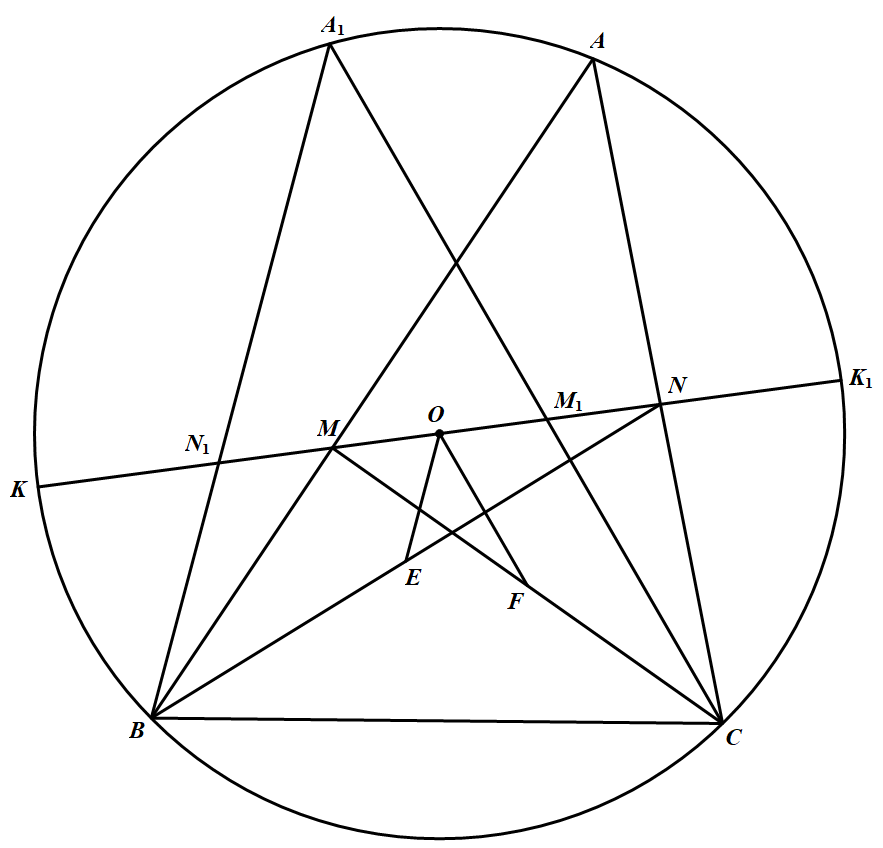
分三种情况考虑，对于直角三角形 $ABC$，结论是显然的，事实 上．如图
若 $\angle ABC$ 为直角，则外心 $O$ 是斜边 $AC$ 的中点，过 $O$ 的直线交 $AB、AC$ 于 $M、N$，则 $O、N$ 共点，由于 $F$ 是 $CM$ 的中 点．故中位线 $OF\parallel AM$，所以 $\angle EOF=\angle OBA=\angle OAB=\angle A$；以下考虑 $\triangle ABC$ 为锐角三角形或钝角三角形的情况（如下图）．
先证引理：如图，过 $\odot O$ 的直径 $KL$ 上的两点 $A,B$ 分别作弦 $CD,EF$，连结 $CE,DF$，分别交 $KL$ 于 $M,N$，若 $OA=OB$，则 $MA=NB$．引理证明：设 $CD $ 交 $EF$ 于点 $ P$，直线 $CE、DF$ 分别截 $\triangle PAB$，据梅涅劳斯定理，$\dfrac{A C}{C P} \cdot \dfrac{P E}{E B} \cdot \dfrac{B M}{M A}=1,\dfrac{B F}{F P} \cdot \dfrac{P D}{D A} \cdot \dfrac{A N}{N B}=1$；则 $\dfrac{M A}{N B}=\dfrac{A C \cdot A D \cdot P E \cdot P F \cdot B M}{B E \cdot B F \cdot P C \cdot P D \cdot A N}$ ①
而由相交弦，得 $P C \cdot P D=P E \cdot P F$ ②
若 $\odot O$ 的半径为 $R,QA= OB= a$，则 $A C \cdot A D=A K \cdot A L=R^{2}-a^{2}=B K \cdot B L=B E \cdot B F$ ③
据 ①②③ 得，$\dfrac{M A}{N B}=\dfrac{M B}{N A}$，即 $\dfrac{M A}{N B}=\dfrac{M A+A B}{N B+A B}=\dfrac{A B}{A B}=1$．
因此 $MA=NB$．引理得证．
回到本题，如下图（两图都适用），延长 $MN$ 得直径 $KK_1$，在直径上取点 $M_1$，使 $OM_1=OM$，设 $CM_1\bigcap \odot O=A_1$，连 $A_1B$ 交 $KK_1$ 于 $N_1$．由引理，$MN_1= M_1N$（下二图中则是 $M_1N_1=MN$）．因此，$O$ 是 $NN_1$ 的中点，故 $OE、OF$ 分别是 $\triangle NBN_1$ 及 $\triangle MCM_1$ 的中位线，于是得 $\angle EOF=\angle BA_1C=\angle A$．
答案
解析
备注
