设 $A A_{0} ,B B_{0}, C C_{0}$ 是 $\triangle A B C$ 的三条角平分线,自 $A_0$ 作 $A_{0} A_{1} / / B B_{0}, A_{0} A_{2} / / C C_{0}$,$A_1、A_2$ 分别在 $AC、AB$ 上,直线 $A_{1} A_{2}$ 交 $BC$ 于 $A_3$;类似得到点 $B_3、C_3$.证明:$A_{3}, B_{3}, C_{3}$ 三点共线.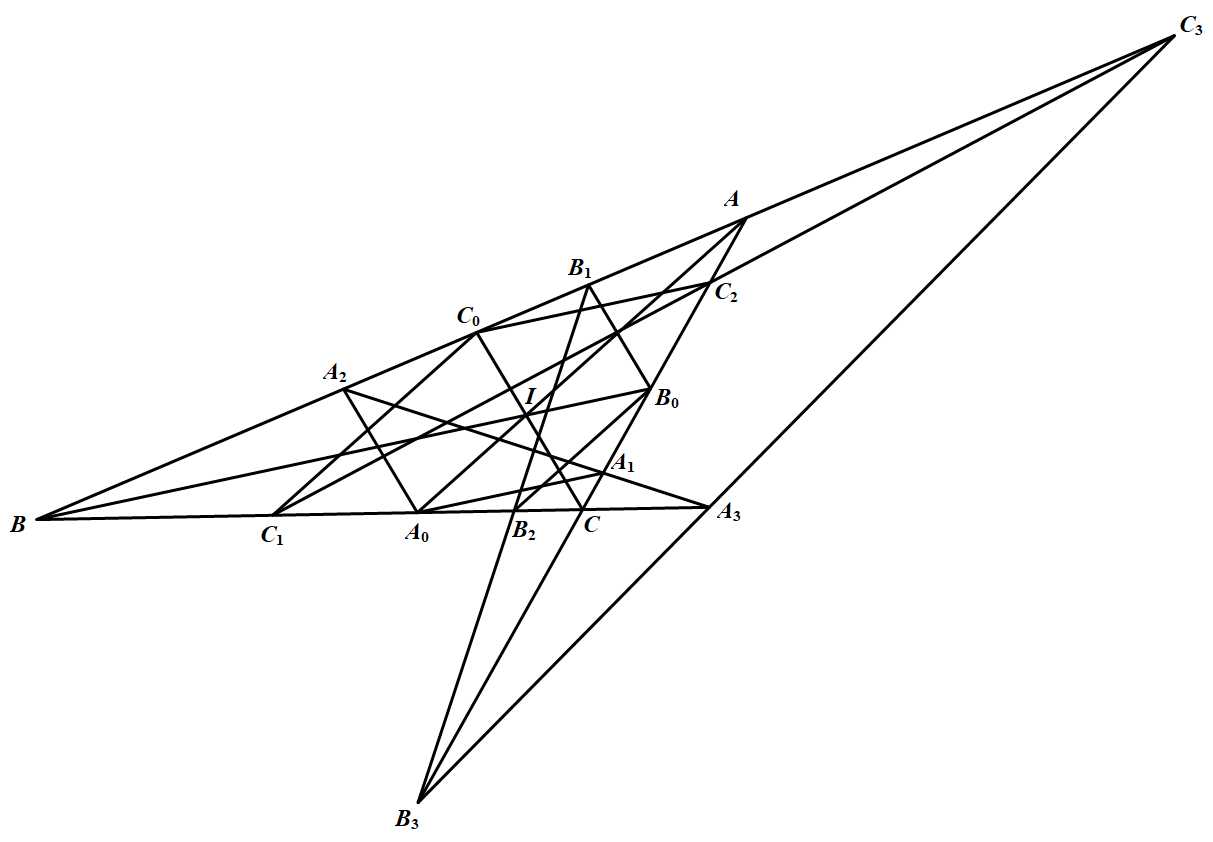

【难度】
【出处】
2011中国东南数学奥林匹克试题
【标注】
【答案】
略
【解析】
据梅涅劳斯逆定理,只要证:$\dfrac{A B_{3}}{B_{3} C} \cdot \dfrac{C A_{3}}{A_{3} B} \cdot \dfrac{B C_{3}}{C_{3} A}=1$ ①
由于直线 $A_1A_2A_3$ 截 $\triangle ABC$,得 $\dfrac{C A_{3}}{A_{3} B} \cdot \dfrac{B A_{2}}{A_{2} A} \cdot \dfrac{A A_{1}}{A_{1} C}=1$
所以 $\dfrac{C A_{3}}{A_{3} B}=\dfrac{A_{2} A}{B A_{2}} \cdot \dfrac{A_{1} C}{A A_{1}}$ ②
同理有 $\dfrac{A B_{3}}{B_{3} C}=\dfrac{B_{2} B}{C B_{2}} \cdot \dfrac{B_{1} A}{B B_{1}}$ ③
$\dfrac{B C_{3}}{C_{3} A}=\dfrac{C_{2} C}{A C_{2}} \cdot \dfrac{C_{1} B}{C C_{1}}$ ④
由 $B A_{2}=\dfrac{B C_{0}}{B C} \cdot B A_{0}, A A_{2}=\dfrac{A A_{0}}{A I} \cdot A C_{0}$,得
$\dfrac{A A_{2}}{B A_{2}}=\dfrac{A A_{0} \cdot A C_{0}}{B A_{0} \cdot B C_{0}} \cdot \dfrac{B C}{A I}$ ⑤
又由 $A A_{1}=\dfrac{A A_{0}}{A I} \cdot A B_{0}, C A_{1}=\dfrac{C A_{0}}{C B} \cdot C B_{0}$,得
$\dfrac{A_{1} C}{A A_{1}}=\dfrac{C A_{0}\cdot C B_{0}}{A A_{0}\cdot A B_{0}} \cdot \dfrac{A I}{B C}$ ⑥
据 ②、⑤、⑥ 得 $\dfrac{C A_{3}}{A_{3} B}=\dfrac{C A_{0}}{B A_{0}} \cdot \dfrac{A C_{0}}{B C_{0}} \cdot \dfrac{C B_{0}}{A B_{0}}=\left(\dfrac{C A_{0}}{A_{0} B}\right)^{2}$.
同理可得,$\dfrac{C B_{3}}{B_{3} A}=\left(\dfrac{C B_{0}}{B_{0} A}\right)^{2},\dfrac{A C_{3}}{C_{3} B}=\left(\dfrac{A C_{0}}{C_{0} B}\right)^{2}$ ⑦
由于 $\triangle ABC$ 的三条角平分线 $A A_{0}, B B_{0}, C C_{0}$ 共点,由塞瓦定理 $\dfrac{A B_{0}}{B_{0} C} \cdot \dfrac{C A_{0}}{A_{0} B} \cdot \dfrac{B C_{0}}{C_{0} A}=1$ ①
于是由 ⑦,⑧ 得 $\dfrac{A B_{3}}{B_{3} C} \cdot \dfrac{C A_{3}}{A_{3} B} \cdot \dfrac{B C_{3}}{C_{3} A}=\left(\dfrac{A B_{0}}{B_{0} C} \cdot \dfrac{C A_{0}}{A_{0} B} \cdot \dfrac{B C_{0}}{C_{0} A}\right)^{2}=1$
即 ① 成立.因此结论得证.
由于直线 $A_1A_2A_3$ 截 $\triangle ABC$,得 $\dfrac{C A_{3}}{A_{3} B} \cdot \dfrac{B A_{2}}{A_{2} A} \cdot \dfrac{A A_{1}}{A_{1} C}=1$
所以 $\dfrac{C A_{3}}{A_{3} B}=\dfrac{A_{2} A}{B A_{2}} \cdot \dfrac{A_{1} C}{A A_{1}}$ ②
同理有 $\dfrac{A B_{3}}{B_{3} C}=\dfrac{B_{2} B}{C B_{2}} \cdot \dfrac{B_{1} A}{B B_{1}}$ ③
$\dfrac{B C_{3}}{C_{3} A}=\dfrac{C_{2} C}{A C_{2}} \cdot \dfrac{C_{1} B}{C C_{1}}$ ④
由 $B A_{2}=\dfrac{B C_{0}}{B C} \cdot B A_{0}, A A_{2}=\dfrac{A A_{0}}{A I} \cdot A C_{0}$,得
$\dfrac{A A_{2}}{B A_{2}}=\dfrac{A A_{0} \cdot A C_{0}}{B A_{0} \cdot B C_{0}} \cdot \dfrac{B C}{A I}$ ⑤
又由 $A A_{1}=\dfrac{A A_{0}}{A I} \cdot A B_{0}, C A_{1}=\dfrac{C A_{0}}{C B} \cdot C B_{0}$,得
$\dfrac{A_{1} C}{A A_{1}}=\dfrac{C A_{0}\cdot C B_{0}}{A A_{0}\cdot A B_{0}} \cdot \dfrac{A I}{B C}$ ⑥
据 ②、⑤、⑥ 得 $\dfrac{C A_{3}}{A_{3} B}=\dfrac{C A_{0}}{B A_{0}} \cdot \dfrac{A C_{0}}{B C_{0}} \cdot \dfrac{C B_{0}}{A B_{0}}=\left(\dfrac{C A_{0}}{A_{0} B}\right)^{2}$.
同理可得,$\dfrac{C B_{3}}{B_{3} A}=\left(\dfrac{C B_{0}}{B_{0} A}\right)^{2},\dfrac{A C_{3}}{C_{3} B}=\left(\dfrac{A C_{0}}{C_{0} B}\right)^{2}$ ⑦
由于 $\triangle ABC$ 的三条角平分线 $A A_{0}, B B_{0}, C C_{0}$ 共点,由塞瓦定理 $\dfrac{A B_{0}}{B_{0} C} \cdot \dfrac{C A_{0}}{A_{0} B} \cdot \dfrac{B C_{0}}{C_{0} A}=1$ ①
于是由 ⑦,⑧ 得 $\dfrac{A B_{3}}{B_{3} C} \cdot \dfrac{C A_{3}}{A_{3} B} \cdot \dfrac{B C_{3}}{C_{3} A}=\left(\dfrac{A B_{0}}{B_{0} C} \cdot \dfrac{C A_{0}}{A_{0} B} \cdot \dfrac{B C_{0}}{C_{0} A}\right)^{2}=1$
即 ① 成立.因此结论得证.
答案
解析
备注