在 $\vartriangle ABC$ 中,$AB=13 BC=14 CA=15$.$G$ 是三角形的重心,点 ${{A}^{\prime }} {{B}^{\prime }} {{C}^{\prime }}$ 分别四点 $A B C$ 绕点 $G$ 旋转 $180{}^\circ $ 所对应的点.求:$\vartriangle ABC$ 与 $\vartriangle {{A}^{\prime }}{{B}^{\prime }}{{C}^{\prime }}$ 所围成区域的面积.
【难度】
【出处】
2003年第21届美国数学邀请赛Ⅱ(AIMEⅡ)
【标注】
【答案】
112
【解析】
如图21-9所示,设 $M$ 是 $BC$ 的中点,${{M}^{\prime }}$ 是 $M$ 关于点 $G$ 的对称点,由于 $M$ 是 $BC$ 的中点,故 ${{M}^{\prime }}$ 是 ${{B}^{\prime }}{{C}^{\prime}}$ 的中点.设 $O,R$ 分别是 ${{A}^{\prime}}{{C}^{\prime }}$,${{A}^{\prime }}{{B}^{\prime }}$ 与 $BC$ 的交点.因为 $BC\parallel {{B}^{\prime}}{{C}^{\prime }}$,故 $\Delta {{A}^{\prime}}RQ\tilde{ }\Delta {{A}^{\prime }}{{B}^{\prime }}{{C}^{\prime }}$.再由 $MG={{M}^{\prime}}G=\dfrac{1}{3}{{A}^{\prime }}{{M}^{\prime }}$ 知 ${{A}^{\prime}}M=\dfrac{1}{3}{{A}^{\prime }}{{M}^{\prime }}$,故 ${{S}_{\vartriangle {{A}^{^{\prime }}}RQ}}=\dfrac{1}{9},{{S}_{\vartriangle {{A}^{^{\prime}}}{{B}^{^{\prime }}},{{C}^{^{\prime }}}}}=\dfrac{1}{9}{{S}_{\vartriangle ABC}}$.同理可知另外两个小三角形的面积也是 $\vartriangle ABC$ 面积的 $\dfrac{1}{9}$.
因此,所求的面积 $S={{S}_{\vartriangle ABC}}\left( 1+\dfrac{1}{9}\cdot 3 \right)=\dfrac{4}{3}{{S}_{\vartriangle ABC}}$.
根据海伦公式,可知 ${{S}_{\vartriangle ABC}}=\sqrt{s\left( s-a \right)\left( a-b \right)\left( a-c \right)}=84$,所以 $S=112$.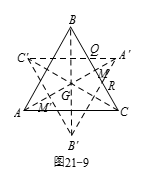
因此,所求的面积 $S={{S}_{\vartriangle ABC}}\left( 1+\dfrac{1}{9}\cdot 3 \right)=\dfrac{4}{3}{{S}_{\vartriangle ABC}}$.
根据海伦公式,可知 ${{S}_{\vartriangle ABC}}=\sqrt{s\left( s-a \right)\left( a-b \right)\left( a-c \right)}=84$,所以 $S=112$.

答案
解析
备注