如图,已知 $\triangle ABC$ 内切圆 $I$ 分别与边 $AB,BC$ 相交于点 $F,D$,直线 $AD,CF$ 分别交圆 $I$ 于另一点 $H,K$.求证:$\dfrac{FD\times HK}{FH\times DK}=3$.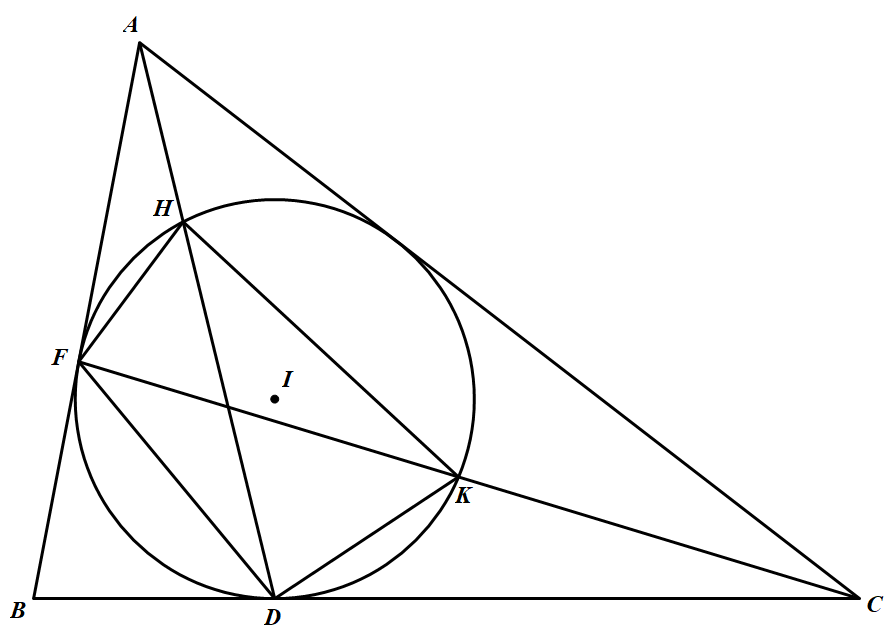

【难度】
【出处】
2010中国东南数学奥林匹克试题
【标注】
【答案】
略
【解析】
证法一
设 $AF=x,BF=y,CD=z$,则可以将各线段长用 $x,y,z$ 表示如下:
由stewart定理得:
$\begin{aligned}
AD^2&=\frac{BD}{BC}\cdot AC^2+\frac{CD}{BC}\cdot AB^2-BD\cdot DC\\
&=\frac{y(x+z)^2+z(x+y)^2}{y+z}-yz\\
&=x^2+\frac{4xyz}{y+z}
\end{aligned}$
由切割线定理得:$AH=\dfrac{AF^2}{AD}=\dfrac{x^2}{AD}$,所以
$HD=AD-AH=\dfrac{AD^2-x^2}{AD}=\dfrac{4xyz}{AD(y+z)}$,
同理有 $KF=\dfrac{4xyz}{CF(x+y)}$.
由 $\triangle CDK\sim\triangle CFD$ 得 $DK=\dfrac{DF\times CD}{CF}=\dfrac{DF}{CF}z$
由 $\triangle AFH\sim\triangle ADF$ 得 $FH=\dfrac{DF\times AF}{AD}=\dfrac{DF}{AD}x$
由余弦定理得
$\begin{aligned}
DF^2&=BD^2+BF^2-2BD\cdot BF\cos B\\
&=2y^2\left(1-\frac{(y+z)^2+(x+y)^2-(x+z)^2}{2(x+y)(y+z)}\right)\\
&=\frac{4xy^2z}{(x+y)(y+z)}
\end{aligned}$
于是
$\begin{aligned}
\frac{KF\times HD}{FH\times DK}&=\frac{\frac{4xyz}{CF(x+y)}\cdot\frac{4xyz}{AD(y+z)}}{\frac{DF}{AD}x\cdot\frac{DF}{CF}z}=\frac{16xy^2z}{DF^2(x+y)(y+z)}=4
\end{aligned}$
对圆内接四边形 $DKHF$ 用托勒密定理得 $KF\cdot HD=DF\cdot HK+FH\cdot DK$
结合 $\dfrac{KF\times HD}{FH\times DK}=4$,使得 $\dfrac{FD\times HK}{FH\times DK}=3$.
证法二
先验证一个引理
引理:如图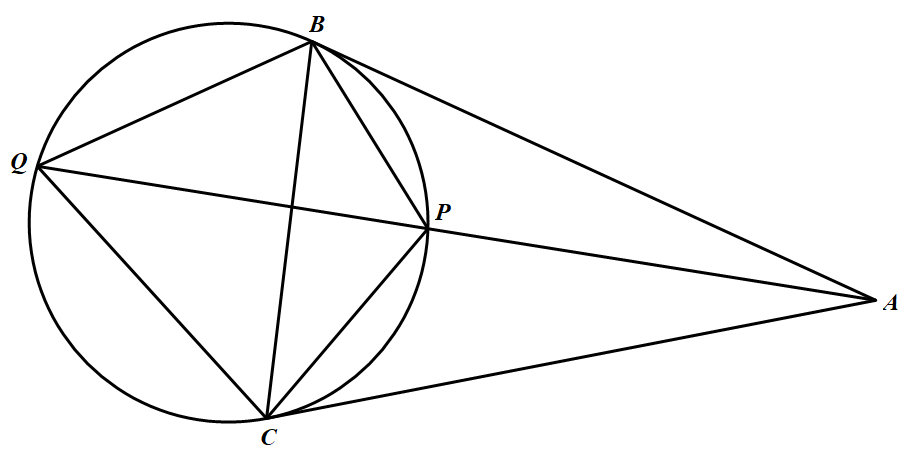 $AB,AC$ 切圆于点 $B,C$,割线 $AP$ 交圆于 点 $ P,Q $ 且点 $ P $ 在 $ A,Q $ 之间.则有 $ PQ\cdot BC=2BP\cdot QC=2BQ\cdot PC $.
$AB,AC$ 切圆于点 $B,C$,割线 $AP$ 交圆于 点 $ P,Q $ 且点 $ P $ 在 $ A,Q $ 之间.则有 $ PQ\cdot BC=2BP\cdot QC=2BQ\cdot PC $.
引理的证明:又托勒密定理知 $ PQ\cdot BC=BP\cdot QC+BQ\cdot PC $.
因 $ AB $ 为圆的切线,故知 $ \angle ABP=\angle AQB$.
再因 $\angle BAP=\angle QAB$,故可得 $\triangle ABP\sim\triangle AQB$,即可得知 $\dfrac{BP}{BQ}=\dfrac{AP}{AB}=\dfrac{AB}{AQ}$.
故 $\left(\dfrac{BP}{BQ}\right)^2=\dfrac{AP}{AB}\times \dfrac{AB}{AQ}=\dfrac{AP}{AQ}$.
同理,$\left(\dfrac{CP}{CQ}\right)^2=\dfrac{AP}{AQ}$.
故知 $\left(\dfrac{CP}{CQ}\right)^2=\left(\dfrac{BP}{BQ}\right)^2$,所以可知 $BP\cdot QC=BQ\cdot PC$,即
$PQ\cdot BC=2BP\cdot QC=2BQ\cdot PC$.
回到原题,设圆 $I$ 与 $AC$ 切于 $Q$ 点并连结 $HQ,QK,QD$ 与 $FQ$,如图.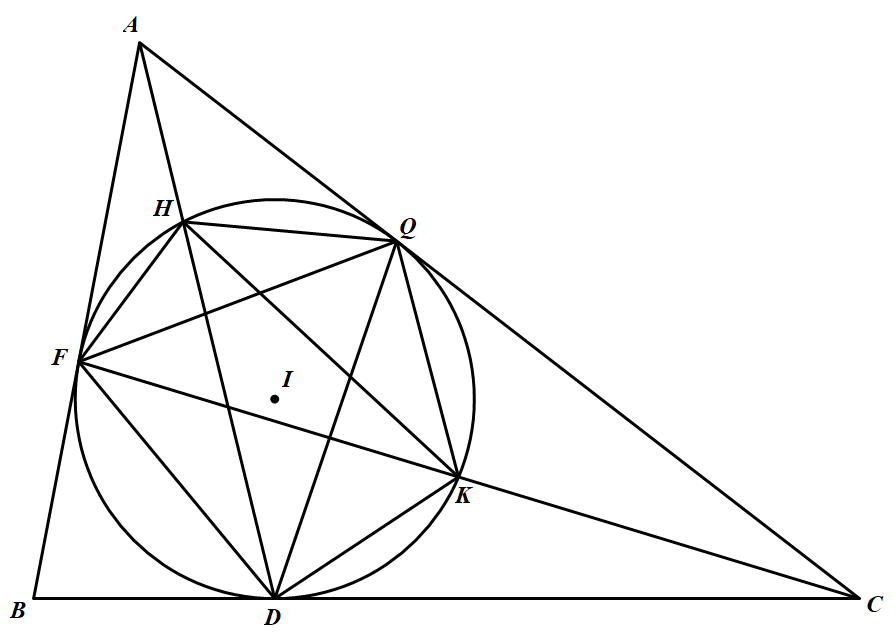 由托勒密定理知 $KF\cdot HD=DF\cdot HK+FH\cdot DK$
由托勒密定理知 $KF\cdot HD=DF\cdot HK+FH\cdot DK$
所以 $\dfrac{FD\times HK}{FH\times DK}=3\Leftrightarrow\dfrac{KF\times HD}{FH\times DK}=4$.
因 $CQ,CD$ 皆为圆 $O$ 的切线,故由引理知
$KF\cdot DQ=2DK\cdot FQ$
$HD\cdot FQ=2FH\cdot DQ$
将以上两式相乘,即得 $KF\cdot HD\cdot DQ\cdot FQ=4DK\cdot FH\cdot DQ\cdot FQ$,即 $\dfrac{KF\times HD}{FH\times DK}=4$.
设 $AF=x,BF=y,CD=z$,则可以将各线段长用 $x,y,z$ 表示如下:
由stewart定理得:
$\begin{aligned}
AD^2&=\frac{BD}{BC}\cdot AC^2+\frac{CD}{BC}\cdot AB^2-BD\cdot DC\\
&=\frac{y(x+z)^2+z(x+y)^2}{y+z}-yz\\
&=x^2+\frac{4xyz}{y+z}
\end{aligned}$
由切割线定理得:$AH=\dfrac{AF^2}{AD}=\dfrac{x^2}{AD}$,所以
$HD=AD-AH=\dfrac{AD^2-x^2}{AD}=\dfrac{4xyz}{AD(y+z)}$,
同理有 $KF=\dfrac{4xyz}{CF(x+y)}$.
由 $\triangle CDK\sim\triangle CFD$ 得 $DK=\dfrac{DF\times CD}{CF}=\dfrac{DF}{CF}z$
由 $\triangle AFH\sim\triangle ADF$ 得 $FH=\dfrac{DF\times AF}{AD}=\dfrac{DF}{AD}x$
由余弦定理得
$\begin{aligned}
DF^2&=BD^2+BF^2-2BD\cdot BF\cos B\\
&=2y^2\left(1-\frac{(y+z)^2+(x+y)^2-(x+z)^2}{2(x+y)(y+z)}\right)\\
&=\frac{4xy^2z}{(x+y)(y+z)}
\end{aligned}$
于是
$\begin{aligned}
\frac{KF\times HD}{FH\times DK}&=\frac{\frac{4xyz}{CF(x+y)}\cdot\frac{4xyz}{AD(y+z)}}{\frac{DF}{AD}x\cdot\frac{DF}{CF}z}=\frac{16xy^2z}{DF^2(x+y)(y+z)}=4
\end{aligned}$
对圆内接四边形 $DKHF$ 用托勒密定理得 $KF\cdot HD=DF\cdot HK+FH\cdot DK$
结合 $\dfrac{KF\times HD}{FH\times DK}=4$,使得 $\dfrac{FD\times HK}{FH\times DK}=3$.
证法二
先验证一个引理
引理:如图
 $AB,AC$ 切圆于点 $B,C$,割线 $AP$ 交圆于 点 $ P,Q $ 且点 $ P $ 在 $ A,Q $ 之间.则有 $ PQ\cdot BC=2BP\cdot QC=2BQ\cdot PC $.
$AB,AC$ 切圆于点 $B,C$,割线 $AP$ 交圆于 点 $ P,Q $ 且点 $ P $ 在 $ A,Q $ 之间.则有 $ PQ\cdot BC=2BP\cdot QC=2BQ\cdot PC $.引理的证明:又托勒密定理知 $ PQ\cdot BC=BP\cdot QC+BQ\cdot PC $.
因 $ AB $ 为圆的切线,故知 $ \angle ABP=\angle AQB$.
再因 $\angle BAP=\angle QAB$,故可得 $\triangle ABP\sim\triangle AQB$,即可得知 $\dfrac{BP}{BQ}=\dfrac{AP}{AB}=\dfrac{AB}{AQ}$.
故 $\left(\dfrac{BP}{BQ}\right)^2=\dfrac{AP}{AB}\times \dfrac{AB}{AQ}=\dfrac{AP}{AQ}$.
同理,$\left(\dfrac{CP}{CQ}\right)^2=\dfrac{AP}{AQ}$.
故知 $\left(\dfrac{CP}{CQ}\right)^2=\left(\dfrac{BP}{BQ}\right)^2$,所以可知 $BP\cdot QC=BQ\cdot PC$,即
$PQ\cdot BC=2BP\cdot QC=2BQ\cdot PC$.
回到原题,设圆 $I$ 与 $AC$ 切于 $Q$ 点并连结 $HQ,QK,QD$ 与 $FQ$,如图.
 由托勒密定理知 $KF\cdot HD=DF\cdot HK+FH\cdot DK$
由托勒密定理知 $KF\cdot HD=DF\cdot HK+FH\cdot DK$所以 $\dfrac{FD\times HK}{FH\times DK}=3\Leftrightarrow\dfrac{KF\times HD}{FH\times DK}=4$.
因 $CQ,CD$ 皆为圆 $O$ 的切线,故由引理知
$KF\cdot DQ=2DK\cdot FQ$
$HD\cdot FQ=2FH\cdot DQ$
将以上两式相乘,即得 $KF\cdot HD\cdot DQ\cdot FQ=4DK\cdot FH\cdot DQ\cdot FQ$,即 $\dfrac{KF\times HD}{FH\times DK}=4$.
答案
解析
备注