如图,三角形 $ABC$ 为直角三角形,$\angle ABC=90^\circ$.$M_1,M_2$ 为 $\triangle ABC$ 内任意两点,$M$ 为线段 $M_1M_2$ 的中点,直线 $BM_1,BM_2,BM$ 与 $AC$ 边分别交于点 $N_1,N_2,N$.求证:$\dfrac{M_1N_1}{BM_1}+\dfrac{M_2N_2}{BM_2}\geqslant 2\dfrac{MN}{BM}$.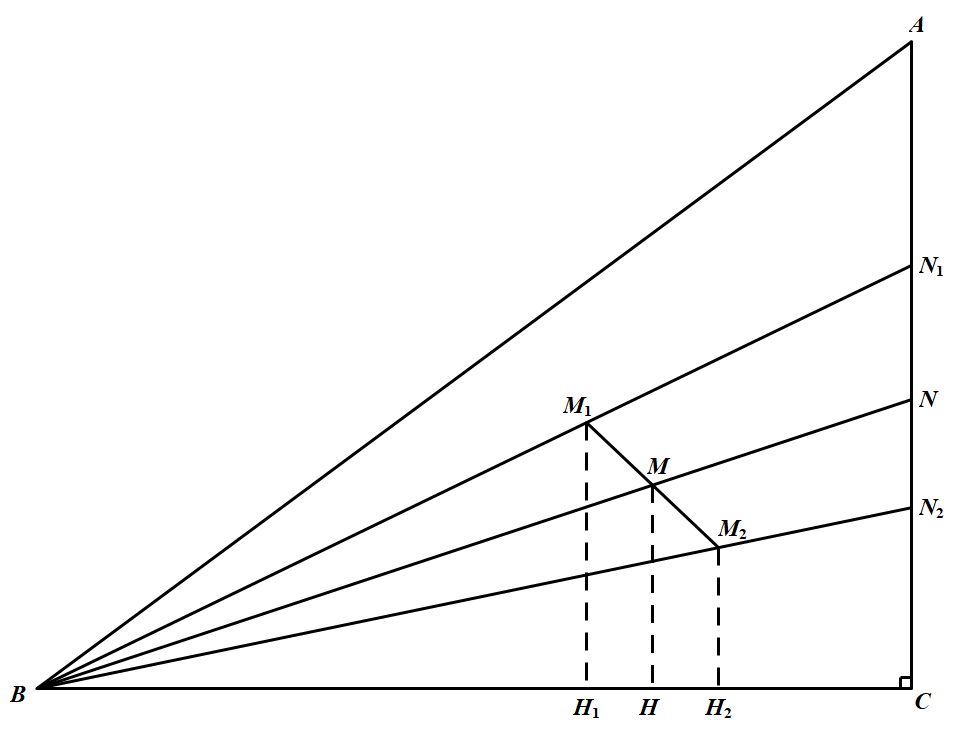

【难度】
【出处】
2010中国东南数学奥林匹克试题
【标注】
【答案】
略
【解析】
设 $H_1,H_2,H$ 分别为点 $M_1,M_2,M$ 在直线 $BC$ 上的投影,则
$\begin{aligned}
\frac{M_1N_1}{BM_1}&=\frac{H_1C}{BH_1}\\
\frac{M_2N_2}{BM_2}&=\frac{H_2C}{BH_2}\\
\frac{MN}{BM}=\frac{HC}{BH}&=\frac{H_1C+H_2C}{BH_1+BH_2}
\end{aligned}$
不妨设 $BC=1,BH_1=x,BH_2=y$,有
$\begin{aligned}
\frac{M_1N_1}{BM_1}=\frac{H_1C}{BH_1}=\frac{1-x}{x}\\
\frac{M_2N_2}{BM_1}=\frac{H_2C}{BH_2}=\frac{1-y}{y}\\
\frac{MN}{BM}=\frac{HC}{BH}=\frac{1-x+1-y}{x+y}
\end{aligned}$
于是,原不等式的证明等价于证明:
$\dfrac{1-x}{x}+\dfrac{1-y}{y}\geqslant 2\dfrac{1-x+1-y}{x+y}$
该不等式等价于 $\dfrac{1}{x}+\dfrac{1}{y}\geqslant \dfrac{4}{x+y}$,即 $(x-y)^2\geqslant 0$.显然成立,故原不等式成立.
$\begin{aligned}
\frac{M_1N_1}{BM_1}&=\frac{H_1C}{BH_1}\\
\frac{M_2N_2}{BM_2}&=\frac{H_2C}{BH_2}\\
\frac{MN}{BM}=\frac{HC}{BH}&=\frac{H_1C+H_2C}{BH_1+BH_2}
\end{aligned}$
不妨设 $BC=1,BH_1=x,BH_2=y$,有
$\begin{aligned}
\frac{M_1N_1}{BM_1}=\frac{H_1C}{BH_1}=\frac{1-x}{x}\\
\frac{M_2N_2}{BM_1}=\frac{H_2C}{BH_2}=\frac{1-y}{y}\\
\frac{MN}{BM}=\frac{HC}{BH}=\frac{1-x+1-y}{x+y}
\end{aligned}$
于是,原不等式的证明等价于证明:
$\dfrac{1-x}{x}+\dfrac{1-y}{y}\geqslant 2\dfrac{1-x+1-y}{x+y}$
该不等式等价于 $\dfrac{1}{x}+\dfrac{1}{y}\geqslant \dfrac{4}{x+y}$,即 $(x-y)^2\geqslant 0$.显然成立,故原不等式成立.
答案
解析
备注