在一个圆周上给定 $8$ 个点 $A_1,A_2,\cdots,A_8$.求最小的正整数 $n$,使得以这 $8$ 个点为顶点的任意 $n$ 个三角形中,必存在两个有公共边的三角形.
【难度】
【出处】
2010中国东南数学奥林匹克试题
【标注】
【答案】
略
【解析】
先考虑两两无公共边的三角形个数 $r$ 的最大值.$8$ 个点,每两点连一条弦,共得 $C_8^2=28$ 条弦,若每条弦只属于一个三角形,则这些弦至多能构成两两无公共边的三角形个数为 $r\leqslant \left[\dfrac{28}{3}\right]=9$ 个,但若有 $9$ 个这样的三角形,共得 $27$ 个顶点,则八边形必有一顶点,至少属于 $4$ 个三角形,设为 $A_8$,共顶点 $A_8$ 的 $4$ 个三角形,$A_8$ 的对边都是 $A_1,A_2,\cdots,A_7$ 之中的两点连线,其中必有一点,设为 $A_k$,出现了两次,那么相应的两个三角形将有一条公共边 $A_8A_k$,这不可能;故 $r\leqslant 8$.
另一方面,当 $r=8$ 时,我们可以作出这样的 $8$ 个三角形,使得其中任两个三角形都无公共边,如:
取圆周的八等分点作为图 $G$ 的八个顶点,作 $8$ 阶完全图,然后去掉其中 $4$ 条直径,这样共得 $24$ 条边,由这些边所构成的三角形中,选取八个等腰三角形:$(1,2,8),(1,3,6),(1,4,7),(2,3,4),(2,5,7),(3,5,8),(4,5,6)$ 以及 $(6,7,8)$,它们两两无公共边.
因此,$r=8$,从而所求的最小值 $n=r+1=9$.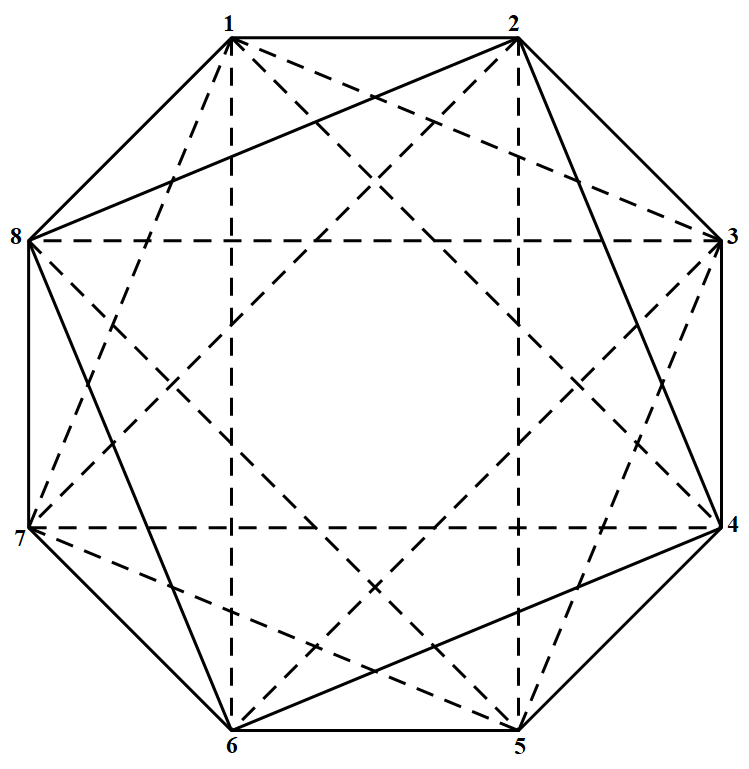
另一方面,当 $r=8$ 时,我们可以作出这样的 $8$ 个三角形,使得其中任两个三角形都无公共边,如:
取圆周的八等分点作为图 $G$ 的八个顶点,作 $8$ 阶完全图,然后去掉其中 $4$ 条直径,这样共得 $24$ 条边,由这些边所构成的三角形中,选取八个等腰三角形:$(1,2,8),(1,3,6),(1,4,7),(2,3,4),(2,5,7),(3,5,8),(4,5,6)$ 以及 $(6,7,8)$,它们两两无公共边.
因此,$r=8$,从而所求的最小值 $n=r+1=9$.

答案
解析
备注