位于 $\vartriangle ABC$ 内的点 $P$ 使得 $\angle PAB$，$\angle PBC$ 及 $\angle PCA$ 全相等．$\vartriangle ABC$ 三边长 $AB=13$，$BC=14$ 及 $CA=15$，且 $\angle PAB$ 的正切为 $\dfrac{m}{n}$，这里 $m$，$n$ 为互素的正整数，求 $m+n$．
【难度】
【出处】
1999年第17届美国数学邀请赛（AIME）
【标注】
【答案】
463
【解析】
设 $\angle PAB=\angle PBC=\angle PCA=\alpha $，$PA=a$，$PB=b$，$PC=c$（如图），于是有
${{S}_{\vartriangle ABC}}=\dfrac{1}{2}\left(13a+14b+15c \right)\sin \alpha $．（1）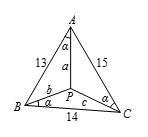
又三角形 $ABC$ 半周长为 $\dfrac{1}{2}\left(13+14+15 \right)=21$，故由海伦公式知
${{S}_{\vartriangle ABC}}=\sqrt{21\left( 21-13 \right)\left( 21-14 \right)\left( 21-15 \right)}=84$．
从而由（1）知 $\left( 13a+14b+15c \right)\sin \alpha =168$．（2）
另一方面，由余弦定理有
$169+{{a}^{2}}-26a\cos \alpha ={{b}^{2}}$，
$196+{{b}^{2}}-28b\cos \alpha ={{c}^{2}}$，
$225+{{c}^{2}}-30c\cos \alpha ={{a}^{2}}$．
三式相加可得 $\left(13a+14b+15c \right)\cos \alpha =295$．（3）
由（2）、（3）即得 $\tan\alpha =\dfrac{168}{295}$．
从而 $m+n=168+295=463$．
${{S}_{\vartriangle ABC}}=\dfrac{1}{2}\left(13a+14b+15c \right)\sin \alpha $．（1）
又三角形 $ABC$ 半周长为 $\dfrac{1}{2}\left(13+14+15 \right)=21$，故由海伦公式知${{S}_{\vartriangle ABC}}=\sqrt{21\left( 21-13 \right)\left( 21-14 \right)\left( 21-15 \right)}=84$．
从而由（1）知 $\left( 13a+14b+15c \right)\sin \alpha =168$．（2）
另一方面，由余弦定理有
$169+{{a}^{2}}-26a\cos \alpha ={{b}^{2}}$，
$196+{{b}^{2}}-28b\cos \alpha ={{c}^{2}}$，
$225+{{c}^{2}}-30c\cos \alpha ={{a}^{2}}$．
三式相加可得 $\left(13a+14b+15c \right)\cos \alpha =295$．（3）
由（2）、（3）即得 $\tan\alpha =\dfrac{168}{295}$．
从而 $m+n=168+295=463$．
答案
解析
备注
