在凸五边形 $ABCDE$ 中,已知 $AB=DE,BC=EA,AB\ne EA$,且 $B,C,D,E$ 四点共圆.
证明:$A,B,C,D$ 四点共圆的充分必要条件是 $AC=AD$.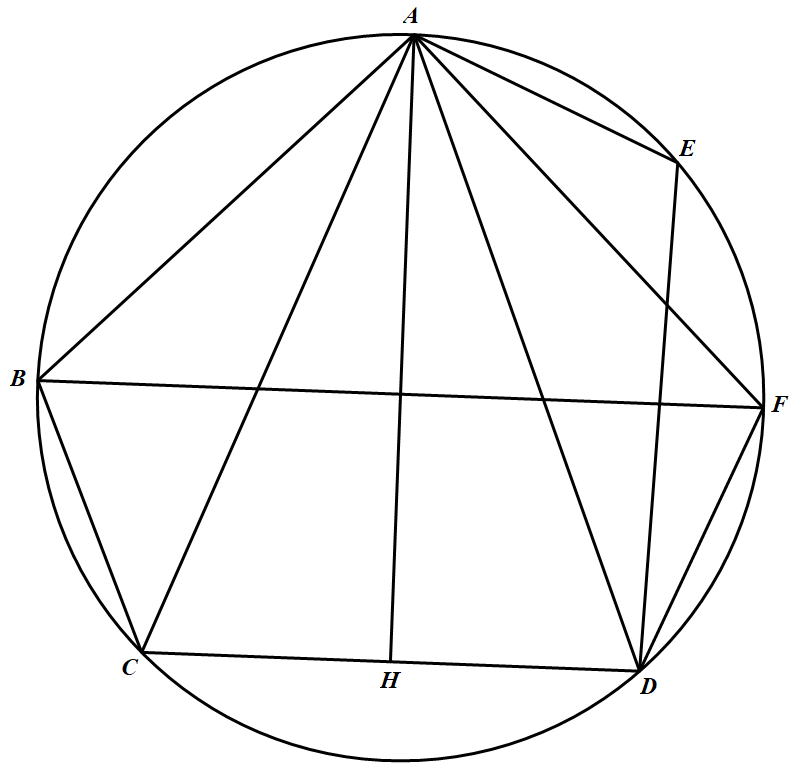
证明:$A,B,C,D$ 四点共圆的充分必要条件是 $AC=AD$.

【难度】
【出处】
2009中国东南数学奥林匹克试题
【标注】
【答案】
略
【解析】
必要性:若 $A,B,C,D$ 共圆,则由 $AB=DE,BC=EA$,得 $\angle BAC=\angle EDA,\angle ACB=\angle DAE$,所以 $\angle ABC=\angle DEA$,故得 $AC=AD$.
充分性:记 $B,C,D,E$ 所共的圆为 $\odot O$,若 $AC=AD$,则圆心 $O$ 在 $CD$ 的中垂线 $AH$ 上.设点 $B$ 关于 $AH$ 的对称点为 $F$,则 $F$ 在 $\odot O$ 上,且因 $AB\ne EA$,即 $DE\ne DF$,所以 $E,F$ 不共点,且 $\triangle AFD\cong \triangle ABC$.又由 $AB=DE,BD=EA$,知 $\triangle AED\cong\triangle CBA$,因此 $\triangle AED\cong\triangle DFA$,故由 $\angle AED=\angle DFA$,得 $A,E,F,D$ 共圆,即点 $A$ 在 $\odot DEF$ 上,也即点 $A$ 在 $\odot O$ 上,从而 $A,B,C,D$ 共圆.
充分性:记 $B,C,D,E$ 所共的圆为 $\odot O$,若 $AC=AD$,则圆心 $O$ 在 $CD$ 的中垂线 $AH$ 上.设点 $B$ 关于 $AH$ 的对称点为 $F$,则 $F$ 在 $\odot O$ 上,且因 $AB\ne EA$,即 $DE\ne DF$,所以 $E,F$ 不共点,且 $\triangle AFD\cong \triangle ABC$.又由 $AB=DE,BD=EA$,知 $\triangle AED\cong\triangle CBA$,因此 $\triangle AED\cong\triangle DFA$,故由 $\angle AED=\angle DFA$,得 $A,E,F,D$ 共圆,即点 $A$ 在 $\odot DEF$ 上,也即点 $A$ 在 $\odot O$ 上,从而 $A,B,C,D$ 共圆.
答案
解析
备注