在 $\triangle ABC$ 中,$BC>AB$,$BD$ 平分 $\angle ABC$ 交 $AC$ 于 $D$,如图,$CP$ 垂直 $BD$,垂足为 $P$,$AQ$ 垂直 $BP$,$Q$ 为垂足.$M$ 是 $AC$ 中点,$E$ 是 $BC$ 中点.若 $\triangle PQM$ 的外接圆 $O$ 与 $AC$ 的另一个交点为 $H$.求证:$Q,H,E,M$ 四点共圆.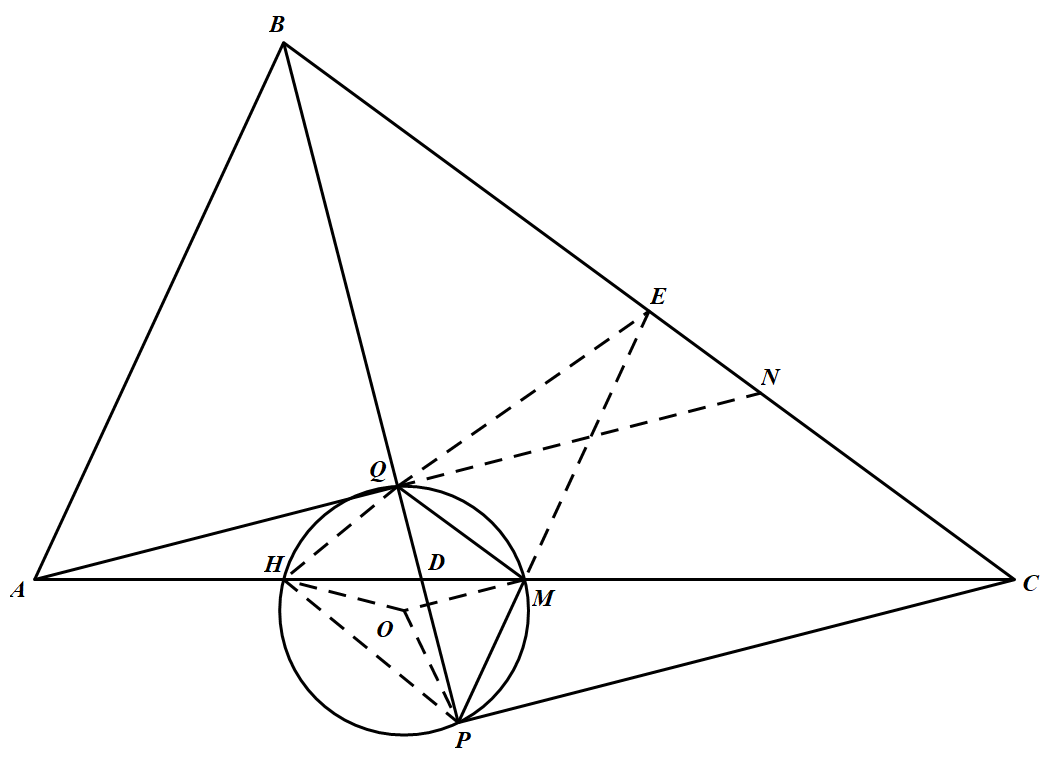

【难度】
【出处】
2008中国东南数学奥林匹克试题
【标注】
【答案】
略
【解析】
作 $AQ$ 延长线交 $BC$ 于 $N$,则 $Q$ 为 $AN$ 中点,又 $M$ 为 $AC$ 中点,所以 $QM\parallel BC$,所以 $\angle PQM=\angle PBC=\dfrac{1}{2}\angle ABC$.
同理 $\angle MPQ=\dfrac{1}{2}\angle ABC$,所以 $QM=PM$.
又因为 $Q,H,P,M$ 共圆,所以 $\angle PHC=\angle PHM=\angle PQM$,得 $\angle PHC=\angle PBC$,所以 $P,H,B,C$ 四点共圆,得 $\angle BHC=\angle BPC=90^\circ$,故 $HE=\dfrac{1}{2}EP$.
结合 $OH=OP$,知 $OE$ 为 $HP$ 中垂线,由 $\angle MPQ=\dfrac{1}{2}\angle ABC$ 及 $E$ 为 $BC$ 的中点可得 $P,M,E$ 共线,故 $\angle EHO=\angle EPO=\angle OPM=\angle OMP$,所以 $O,H,E,M$ 四点共圆.
同理 $\angle MPQ=\dfrac{1}{2}\angle ABC$,所以 $QM=PM$.
又因为 $Q,H,P,M$ 共圆,所以 $\angle PHC=\angle PHM=\angle PQM$,得 $\angle PHC=\angle PBC$,所以 $P,H,B,C$ 四点共圆,得 $\angle BHC=\angle BPC=90^\circ$,故 $HE=\dfrac{1}{2}EP$.
结合 $OH=OP$,知 $OE$ 为 $HP$ 中垂线,由 $\angle MPQ=\dfrac{1}{2}\angle ABC$ 及 $E$ 为 $BC$ 的中点可得 $P,M,E$ 共线,故 $\angle EHO=\angle EPO=\angle OPM=\angle OMP$,所以 $O,H,E,M$ 四点共圆.
答案
解析
备注