如图,$\triangle ABC$ 的内切圆 $I$ 分别切 $BC,AC$ 于点 $M,N$,$E,F$ 分别为边 $AB,AC$ 的中点,$D$ 是直线 $EF$ 与 $BI$ 的交点.证明;$M,N,D$ 三点共线.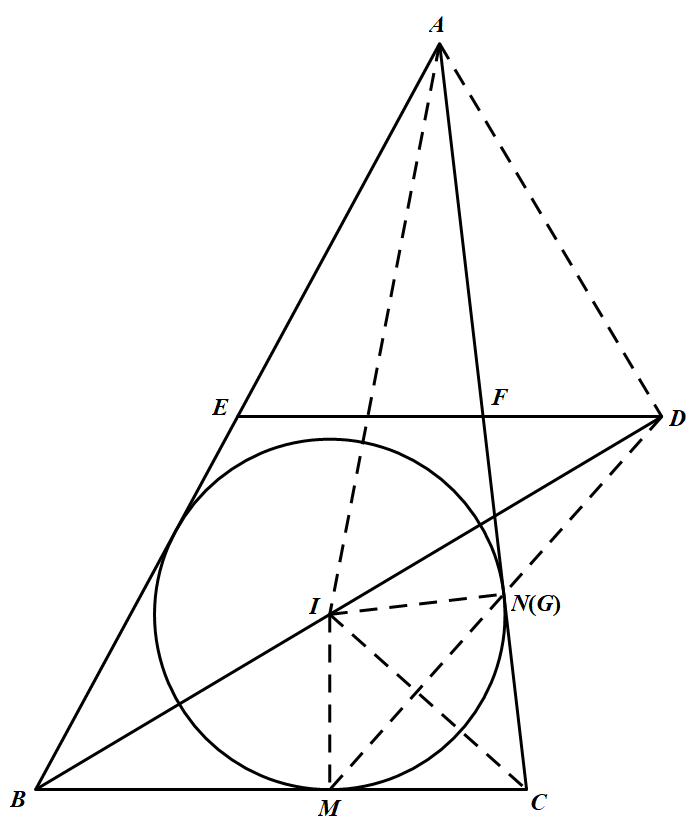

【难度】
【出处】
2008中国东南数学奥林匹克试题
【标注】
【答案】
略
【解析】
连结 $AD$,则易知 $\angle ADB=90^\circ$.并连接 $AI,DM$,$DM$ 与 $AC$ 交于点 $G$.因为 $\angle ABI=\angle DBM$,所以 $\dfrac{AB}{BD}=\dfrac{BI}{BM}$,故 $\triangle ABI\sim\triangle DBM$,从而 $\angle DMB=\angle AIB=90^\circ+\dfrac{1}{2}\angle ACB$
连结 $IG,IC,IM$,则 $\angle IMG=\angle DMB-90^\circ=\dfrac{1}{2}\angle ACB=\angle GCI$,所以 $I,M,C,G$ 四点共圆.
从而 $IG\perp AC$,因此 $G$ 与 $N$ 重合,即 $M,N,D$ 三点共线.
连结 $IG,IC,IM$,则 $\angle IMG=\angle DMB-90^\circ=\dfrac{1}{2}\angle ACB=\angle GCI$,所以 $I,M,C,G$ 四点共圆.
从而 $IG\perp AC$,因此 $G$ 与 $N$ 重合,即 $M,N,D$ 三点共线.
答案
解析
备注