如图所示，设 $C,D$ 是以 $O$ 为圆心，$AB$ 为直径的半圆上的任意两点，过点 $B$ 作 $\odot O$ 的切线交直线 $CD$ 于 $P$，直线 $PO$ 与直线 $CA,AD$ 分别交于点 $E,F$．
证明：$OE=OF$．
证明：$OE=OF$．
【难度】
【出处】
2007中国东南数学奥林匹克试题
【标注】
【答案】
略
【解析】
证法一
如图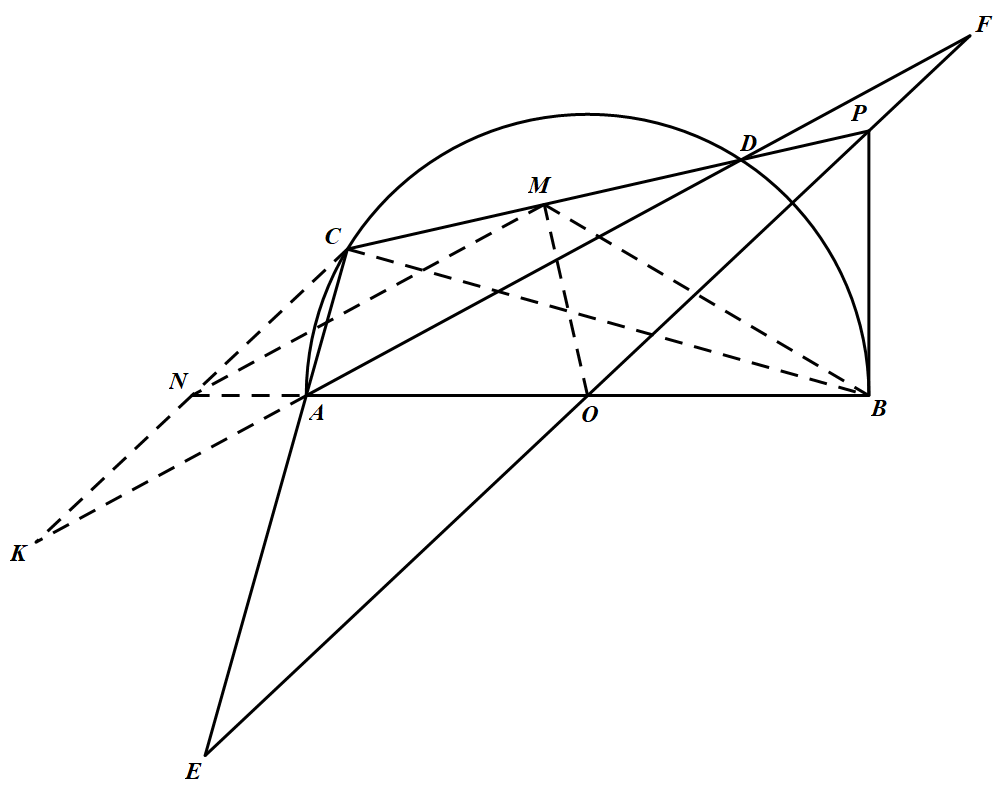
作 $OM\perp CD$ 于 $M$，作 $MN\parallel AD$，设 $MN\bigcap BA=N,CN\bigcap DA=K$，连 $BC,BM$，则 $\angle NBC=\angle ADC=\angle NMC$，因此 $N,B,M,C$ 共圆；又由 $O,B,P,M$ 共圆，得 $\angle OPM=\angle OBM=180^\circ-\angle MCN$，所以 $CN\parallel OP$，于是 $\dfrac{CN}{OE}=\dfrac{AN}{AO}=\dfrac{NK}{OF}$ ①
因 $M$ 为 $CD$ 的中点，$MN\parallel DK$，则 $N$ 为 $CK$ 的中点；故由 ① 得，$OE=OF$．
证法二
如图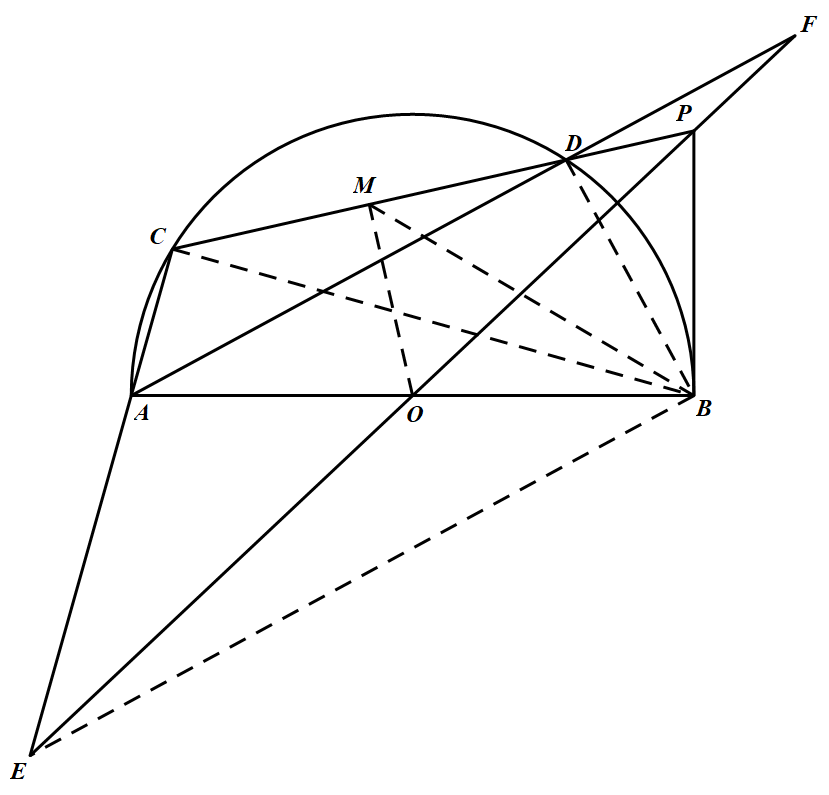
如图，过 $O$ 作 $OM\perp CD$ 于 $M$，连结 $BC,BM,BD,BE$，因为 $OM\perp CD,PB\perp AB$，所以 $O,B,P,M$ 四点共圆，于是 $\angle BMP=\angle BOP=\angle AOE,\angle EAO=\angle BDM$
所以 $\triangle OAE\sim\triangle MDB,\dfrac{AE}{BD}=\dfrac{AO}{DM}=\dfrac{AB}{CD}$
从而 $\triangle BAE\sim\triangle CDB,\angle EBA=\angle BCD=\angle BAD$
所以 $AD\parallel BE,\dfrac{OE}{OF}=\dfrac{OB}{OA}=1$，即 $OE=OF$．
如图
作 $OM\perp CD$ 于 $M$，作 $MN\parallel AD$，设 $MN\bigcap BA=N,CN\bigcap DA=K$，连 $BC,BM$，则 $\angle NBC=\angle ADC=\angle NMC$，因此 $N,B,M,C$ 共圆；又由 $O,B,P,M$ 共圆，得 $\angle OPM=\angle OBM=180^\circ-\angle MCN$，所以 $CN\parallel OP$，于是 $\dfrac{CN}{OE}=\dfrac{AN}{AO}=\dfrac{NK}{OF}$ ①因 $M$ 为 $CD$ 的中点，$MN\parallel DK$，则 $N$ 为 $CK$ 的中点；故由 ① 得，$OE=OF$．
证法二
如图
如图，过 $O$ 作 $OM\perp CD$ 于 $M$，连结 $BC,BM,BD,BE$，因为 $OM\perp CD,PB\perp AB$，所以 $O,B,P,M$ 四点共圆，于是 $\angle BMP=\angle BOP=\angle AOE,\angle EAO=\angle BDM$所以 $\triangle OAE\sim\triangle MDB,\dfrac{AE}{BD}=\dfrac{AO}{DM}=\dfrac{AB}{CD}$
从而 $\triangle BAE\sim\triangle CDB,\angle EBA=\angle BCD=\angle BAD$
所以 $AD\parallel BE,\dfrac{OE}{OF}=\dfrac{OB}{OA}=1$，即 $OE=OF$．
答案
解析
备注
