如图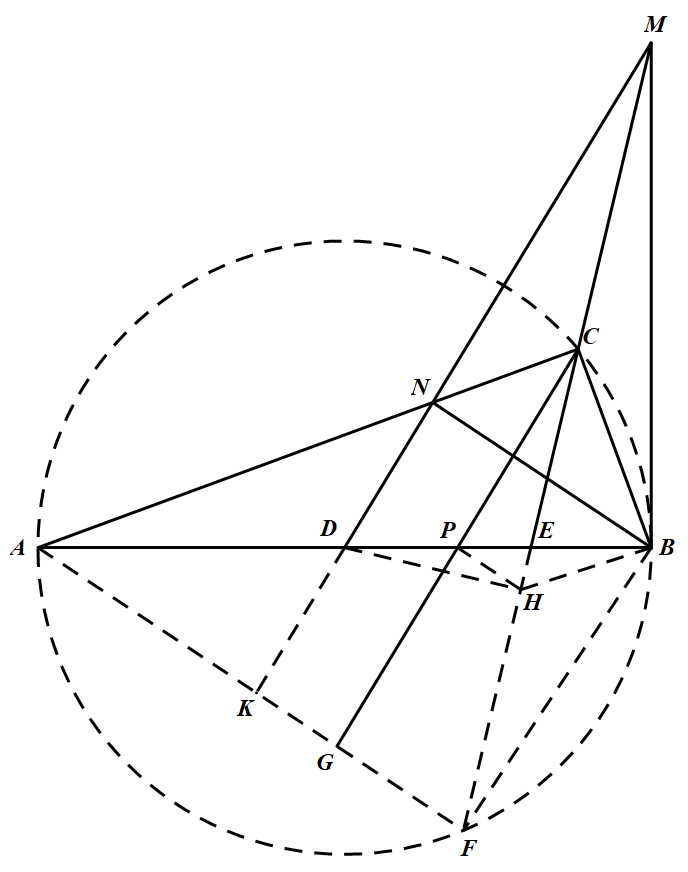
直角三角形 $ABC$ 中，$D$ 是斜边 $AB$ 的中点，$MB\perp AB$，$MD$ 交 $AC$ 于 $N$；$MC$ 的延长线交 $AB$ 于 $E$．证明：$\angle DBN=\angle BCE$．
直角三角形 $ABC$ 中，$D$ 是斜边 $AB$ 的中点，$MB\perp AB$，$MD$ 交 $AC$ 于 $N$；$MC$ 的延长线交 $AB$ 于 $E$．证明：$\angle DBN=\angle BCE$．【难度】
【出处】
2007中国东南数学奥林匹克试题
【标注】
【答案】
略
【解析】
如图，延长 $ME$ 交 $\triangle ABC$ 的外接圆于 $F$，延长 $MD$ 交 $AF$ 于 $K$，作 $CG\parallel MK$，交 $AF$ 于 $G$，交 $AB$ 于 $P$，作 $DH\perp CF$ 于 $H$，则 $H$ 为 $CF$ 的中点．连 $HB,HP$，则 $D,H,B,M$ 共圆，故 $\angle HBD=\angle HMD=\angle HCP$，于是 $H,B,C,P$ 共圆，所以 $\angle PHC=\angle ABC=\angle AFC$，故 $PH\parallel AF$．即 $PH$ 为 $\triangle CFG$ 的中位线，$P$ 是 $CG$ 的中点．则 $AP$ 为 $\triangle ACG$ 的边 $CG$ 上的中线，又因 $NK\parallel CG$，故 $D$ 是 $NK$ 的中点，即线段 $AB$ 与 $NK$ 互相平分，所以 $\angle DBN=\angle DAK$，而 $\angle DAK=\angle BAF=\angle BCF=\angle BCE$，即有 $\angle DBN=\angle BCE$．
答案
解析
备注
