如图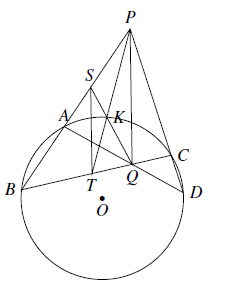
$PAB,PCD$ 是圆 $O$ 的两条割线，$AD,BC$ 相交于点 $Q,T$ 是线段 $BQ$ 上一点，线段 $PT$ 与圆 $O$ 交于点 $K$，直线 $QK$ 与线段 $PA$ 交于点 $S$．证明：若 $ST\parallel PQ$，则 $B,S,K,T$ 四点共圆．
$PAB,PCD$ 是圆 $O$ 的两条割线，$AD,BC$ 相交于点 $Q,T$ 是线段 $BQ$ 上一点，线段 $PT$ 与圆 $O$ 交于点 $K$，直线 $QK$ 与线段 $PA$ 交于点 $S$．证明：若 $ST\parallel PQ$，则 $B,S,K,T$ 四点共圆．【难度】
【出处】
2016中国东南数学奥林匹克试题(高二)
【标注】
【答案】
略
【解析】
如图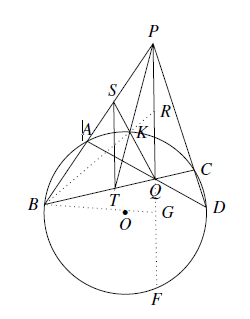
设线段 $PQ$ 与圆 $O$ 交于点 $E$，$PQ$ 的延长线与圆 $O$ 交于点 $F$．则由 $\angle PQA>\angle ADC=\angle ABC$ 知，射线 $PQ$ 上存在一点 $G$，使得 $\angle ABG=\angle PQA$，从而 $A,B,G,Q$ 四点共圆．
故 $
P Q \cdot P G=P A \cdot P B=P E \cdot P F$，且 $\angle PGB=180^{\circ}-\angle BAD=180^{\circ}-\angle BCD=\angle PCB$，从而 $B,G,C,P$ 四点共圆，故又有 $PQ\cdot QG=QC\cdot QB=QE\cdot QF$．
因此 $PQ^2 =PQ\cdot PG-PQ\cdot QG=PE\cdot PF-QE\cdot QF$．
设 $BK$ 延长线与 $PQ$ 交于点 $R$．在 $\triangle PBQ$ 中，由塞瓦定理得
$\dfrac{P R}{R Q} \cdot \dfrac{Q T}{T B} \cdot \dfrac{B S}{S P}=1$ ①
由 $ST\parallel PQ$ 知，$\dfrac{Q T}{T B}=\dfrac{P S}{S B}$ ②
所以 $R$ 是线段 $PQ$ 的中点，因此
$\begin{aligned}
PQ=2RQ,PE=RQ+RE,PF=RQ+RF,QE=RQ-RE,QF=RF-RQ
\end{aligned}$
进而 $\begin{aligned}
4RQ^2 &=(RQ+RE)(RQ+RF)-(RQ-RE)(RF-RQ)=2RQ^2 +2RE\cdot RF
\end{aligned}$
即 $RQ^2 =RE\cdot RF$．又 $RE\cdot RF=RK\cdot RB$，所以 $RQ^2 =RK\cdot RB$，从而 $\triangle RKQ\sim\triangle RQB$．
于是 $\angle KBT=\angle KQR=\angle KST$，因此 $B,S,K,T$ 四点共圆．
设线段 $PQ$ 与圆 $O$ 交于点 $E$，$PQ$ 的延长线与圆 $O$ 交于点 $F$．则由 $\angle PQA>\angle ADC=\angle ABC$ 知，射线 $PQ$ 上存在一点 $G$，使得 $\angle ABG=\angle PQA$，从而 $A,B,G,Q$ 四点共圆．故 $
P Q \cdot P G=P A \cdot P B=P E \cdot P F$，且 $\angle PGB=180^{\circ}-\angle BAD=180^{\circ}-\angle BCD=\angle PCB$，从而 $B,G,C,P$ 四点共圆，故又有 $PQ\cdot QG=QC\cdot QB=QE\cdot QF$．
因此 $PQ^2 =PQ\cdot PG-PQ\cdot QG=PE\cdot PF-QE\cdot QF$．
设 $BK$ 延长线与 $PQ$ 交于点 $R$．在 $\triangle PBQ$ 中，由塞瓦定理得
$\dfrac{P R}{R Q} \cdot \dfrac{Q T}{T B} \cdot \dfrac{B S}{S P}=1$ ①
由 $ST\parallel PQ$ 知，$\dfrac{Q T}{T B}=\dfrac{P S}{S B}$ ②
所以 $R$ 是线段 $PQ$ 的中点，因此
$\begin{aligned}
PQ=2RQ,PE=RQ+RE,PF=RQ+RF,QE=RQ-RE,QF=RF-RQ
\end{aligned}$
进而 $\begin{aligned}
4RQ^2 &=(RQ+RE)(RQ+RF)-(RQ-RE)(RF-RQ)=2RQ^2 +2RE\cdot RF
\end{aligned}$
即 $RQ^2 =RE\cdot RF$．又 $RE\cdot RF=RK\cdot RB$，所以 $RQ^2 =RK\cdot RB$，从而 $\triangle RKQ\sim\triangle RQB$．
于是 $\angle KBT=\angle KQR=\angle KST$，因此 $B,S,K,T$ 四点共圆．
答案
解析
备注
