如图所示,在 $\triangle ABC$ 中,$\angle ABC=90 \circ $,$ D,G $ 是边 $ CA$ 上的两点,连接 $BD,BG$.过点 $A,G$ 分别作 $BD$ 的垂线,垂足分别为 $E,F$,连接 $CF$.已知 $BE=EF$,求证:$\angle ABG=\angle DFC.$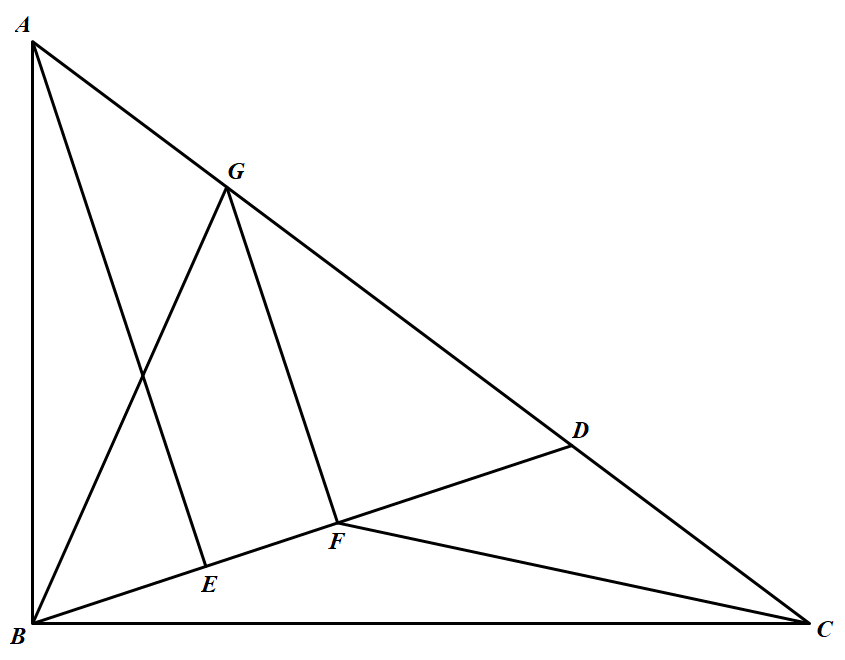

【难度】
【出处】
2006中国东南数学奥林匹克试题
【标注】
【答案】
略
【解析】
证法一
作 $GM\bot AB$ 于 $M$,设 $AE$ 与 $BG$ 的交点为 $K$,连接 $KM$.由 $BE=EF$,及 $AE\parallel GF$ 知,$K$ 为 $Rt\triangle BGM$ 斜边 $BG$ 上的中线,所以 $BK=KG=MK,\angle ABG=\angle BMK$.因为 $BF\cdot AK=4S_{\triangle ABK}=2S_{\triangle ABG}=AB\cdot MG$,又 $MG\parallel BC$,所以 $\dfrac{AB}{BC}=\dfrac{AM}{MG}$,故 $AB\cdot MG=BC\cdot AM$,所以 $BF\cdot AK=BC\cdot AM$,即 $\dfrac{BF}{BC}=\dfrac{AM}{AK}$.
结合 $\angle KAB=\angle CBD$,知 $\triangle KAM\sim\triangle CBF$,所以 $\angle AMK=\angle CFB$,于是 $\angle BMK=\angle CFD$,故 $\angle ABG=\angle DFC$.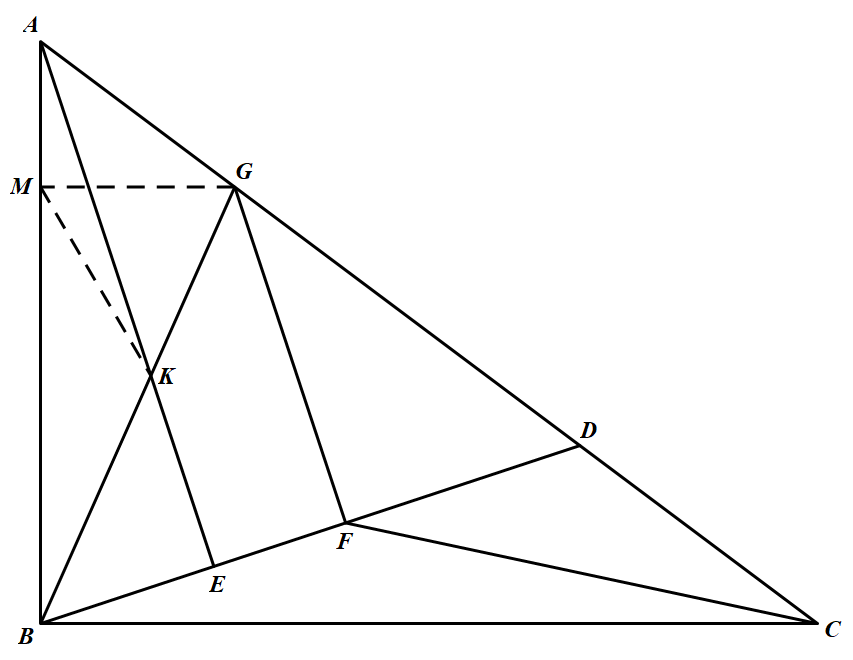 证法二
证法二
作 $Rt\triangle ABC$ 的外接圆 $w$,延长 $BD,AE$ 分别交 $w$ 于 $K,J$.
连接 $BJ,CJ,KJ,FJ$.易知 $\angle BAJ=\angle KBC$,故 $BJ=KC$.于是四边形 $BJCK$ 是等腰梯形,又 $AJ$ 垂直平分 $BF$,故 $BJ=FJ$,故四边形 $FJCK$ 是平行四边形.
设 $AE$ 与 $BG$ 的交点为 $M$,$FC$ 与 $JK$ 的交点为 $N$,则 $M,N$ 分别是 $BG$ 和 $FC$ 的中点,于是 $\dfrac{AB}{AG}=\dfrac{\sin\angle MAG}{\sin\angle BAM}=\dfrac{\sin\angle JKC}{\sin\angle BKJ}=\dfrac{FK}{CK}$.
又 $\angle BAG=\angle FKC$,于是 $\triangle BAG\sim\triangle FKC$,所以 $\angle ABG=\angle DFC$.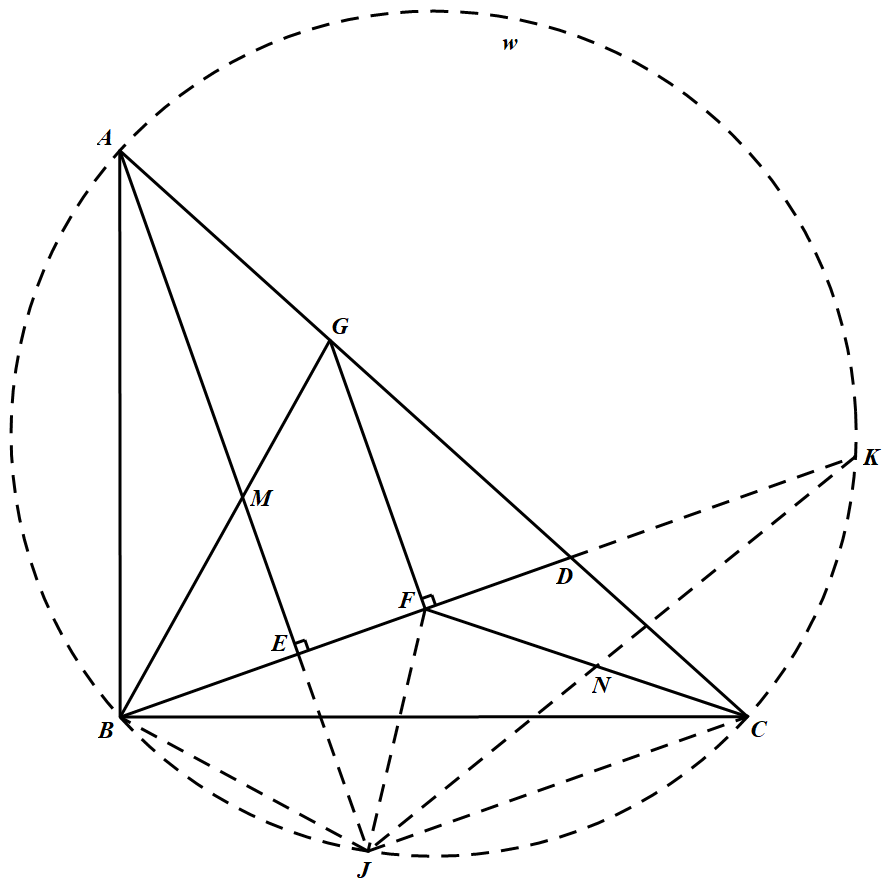
作 $GM\bot AB$ 于 $M$,设 $AE$ 与 $BG$ 的交点为 $K$,连接 $KM$.由 $BE=EF$,及 $AE\parallel GF$ 知,$K$ 为 $Rt\triangle BGM$ 斜边 $BG$ 上的中线,所以 $BK=KG=MK,\angle ABG=\angle BMK$.因为 $BF\cdot AK=4S_{\triangle ABK}=2S_{\triangle ABG}=AB\cdot MG$,又 $MG\parallel BC$,所以 $\dfrac{AB}{BC}=\dfrac{AM}{MG}$,故 $AB\cdot MG=BC\cdot AM$,所以 $BF\cdot AK=BC\cdot AM$,即 $\dfrac{BF}{BC}=\dfrac{AM}{AK}$.
结合 $\angle KAB=\angle CBD$,知 $\triangle KAM\sim\triangle CBF$,所以 $\angle AMK=\angle CFB$,于是 $\angle BMK=\angle CFD$,故 $\angle ABG=\angle DFC$.
 证法二
证法二作 $Rt\triangle ABC$ 的外接圆 $w$,延长 $BD,AE$ 分别交 $w$ 于 $K,J$.
连接 $BJ,CJ,KJ,FJ$.易知 $\angle BAJ=\angle KBC$,故 $BJ=KC$.于是四边形 $BJCK$ 是等腰梯形,又 $AJ$ 垂直平分 $BF$,故 $BJ=FJ$,故四边形 $FJCK$ 是平行四边形.
设 $AE$ 与 $BG$ 的交点为 $M$,$FC$ 与 $JK$ 的交点为 $N$,则 $M,N$ 分别是 $BG$ 和 $FC$ 的中点,于是 $\dfrac{AB}{AG}=\dfrac{\sin\angle MAG}{\sin\angle BAM}=\dfrac{\sin\angle JKC}{\sin\angle BKJ}=\dfrac{FK}{CK}$.
又 $\angle BAG=\angle FKC$,于是 $\triangle BAG\sim\triangle FKC$,所以 $\angle ABG=\angle DFC$.

答案
解析
备注