如图，在 $\triangle ABC$ 中，$\angle A=60^\circ$，$\triangle ABC$ 的内切圆 $I$ 分别切边 $AB,AC$ 于点 $D,E$，直线 $DE$ 分别与直线 $BI,CI$ 相交于点 $F,G$，证明：$FG=\dfrac{1}{2}BC$．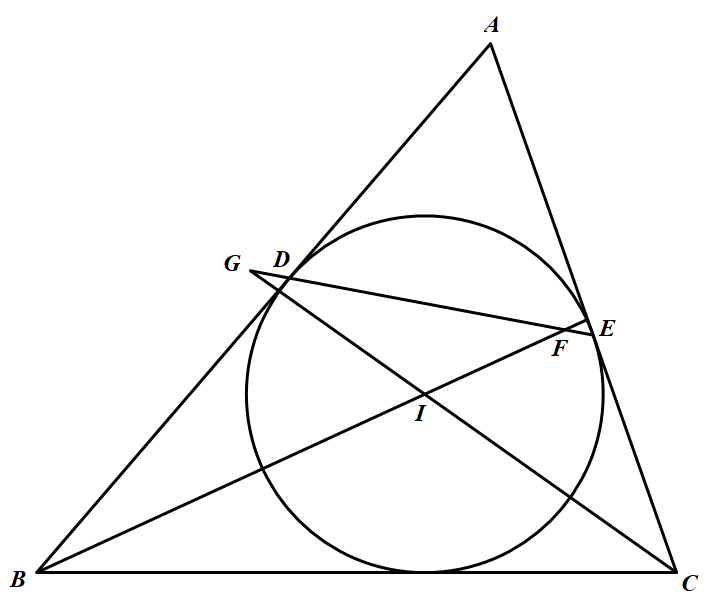
【难度】
【出处】
2006中国东南数学奥林匹克试题
【标注】
【答案】
略
【解析】
证法一
分别连接 $CF,BG,ID,IE,AI$，则 $A,D,I,E$ 四点共圆．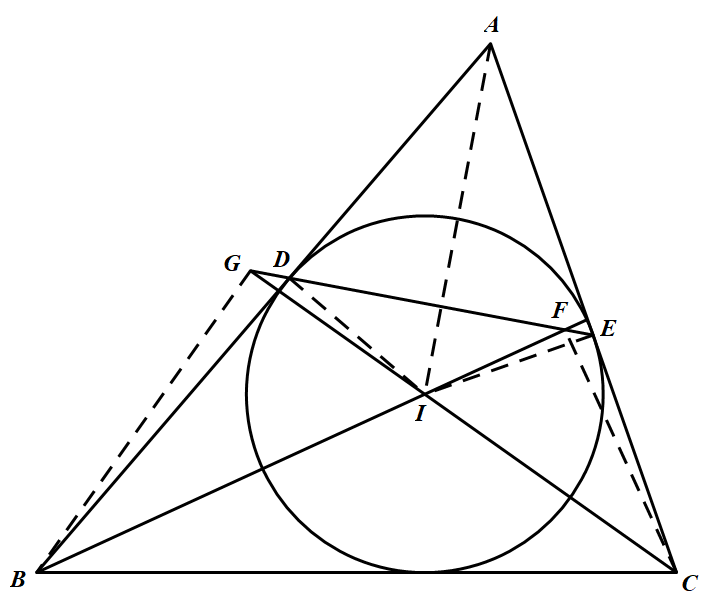
所以 $\angle IDE=\dfrac{1}{2}\angle A$，从而 $\angle BDF=90^\circ+\dfrac{1}{2}\angle A$，又 $\angle BIC=180^\circ-\dfrac{1}{2}(\angle B+\angle C)=90^\circ+\dfrac{1}{2}\angle A$，所以 $\angle BDF=\angle BIC$．
又 $\angle DBF=\angle CBI$，得 $\triangle FDB\sim\triangle CIB$．所以 $\dfrac{FB}{CB}=\dfrac{DB}{IB}$．
又由 $\angle DBI=\angle FBC$，得 $\triangle IDB\sim\triangle CFB$，所以 $CF\perp BF$，从而 $\angle FCG=\dfrac{1}{2}\angle A=30^\circ$．
同理 $BG\perp GC$，所以 $B,C,F,G$ 四点共圆，由此 $\dfrac{FG}{\sin\angle FCG}=BC$，所以 $FG=\dfrac{1}{2}BC$．
证法二
因为 $\angle BIG=\dfrac{1}{2}(\angle B+\angle C)$，又因为 $\angle BDG=\angle ADE=\dfrac{180^\circ-\angle A}{2}=\dfrac{1}{2}(\angle B+\angle C)$，所以 $B,D,I,G$ 四点共圆，因此 $\angle BGC=\angle BDI=90^\circ$．
同理 $\angle CFB=90^\circ$，所以 $B,C,F,G$ 四点共圆．
又 $\angle FCG=90^\circ-\angle FBC-\angle BCI=90^\circ-\dfrac{1}{2}(\angle B+\angle C)=30^\circ$，所以 $FG=BC\cdot\sin\angle FCG=\dfrac{1}{2}BC$．
分别连接 $CF,BG,ID,IE,AI$，则 $A,D,I,E$ 四点共圆．
所以 $\angle IDE=\dfrac{1}{2}\angle A$，从而 $\angle BDF=90^\circ+\dfrac{1}{2}\angle A$，又 $\angle BIC=180^\circ-\dfrac{1}{2}(\angle B+\angle C)=90^\circ+\dfrac{1}{2}\angle A$，所以 $\angle BDF=\angle BIC$．又 $\angle DBF=\angle CBI$，得 $\triangle FDB\sim\triangle CIB$．所以 $\dfrac{FB}{CB}=\dfrac{DB}{IB}$．
又由 $\angle DBI=\angle FBC$，得 $\triangle IDB\sim\triangle CFB$，所以 $CF\perp BF$，从而 $\angle FCG=\dfrac{1}{2}\angle A=30^\circ$．
同理 $BG\perp GC$，所以 $B,C,F,G$ 四点共圆，由此 $\dfrac{FG}{\sin\angle FCG}=BC$，所以 $FG=\dfrac{1}{2}BC$．
证法二
因为 $\angle BIG=\dfrac{1}{2}(\angle B+\angle C)$，又因为 $\angle BDG=\angle ADE=\dfrac{180^\circ-\angle A}{2}=\dfrac{1}{2}(\angle B+\angle C)$，所以 $B,D,I,G$ 四点共圆，因此 $\angle BGC=\angle BDI=90^\circ$．
同理 $\angle CFB=90^\circ$，所以 $B,C,F,G$ 四点共圆．
又 $\angle FCG=90^\circ-\angle FBC-\angle BCI=90^\circ-\dfrac{1}{2}(\angle B+\angle C)=30^\circ$，所以 $FG=BC\cdot\sin\angle FCG=\dfrac{1}{2}BC$．
答案
解析
备注
