如图,圆 $O$(圆心为 $O$)与直线 $l$ 相离,作 $OP\perp l$,$P$ 垂足.设点 $Q$ 是 $l$ 上任意一点(不与点 $P$ 重合),过点 $Q$ 作圆 $O$ 的两条切线 $QA$ 和 $QB$,$A$ 和 $B$ 为切点,$AB$ 与 $OP$ 相交于点 $K$.过点 $P$ 作 $PM\perp QB,PN\perp QA$,$M$ 和 $N$ 为垂足.求证:直线 $MN$ 平分线段 $KP$.
【难度】
【出处】
2005中国东南数学奥林匹克试题
【标注】
【答案】
略
【解析】
作 $PI\perp AB$,$I$ 为垂足,记 $J$ 为直线 $MN$ 与线段 $PK$ 的交点.易知 $\angle QAO=\angle QBD=\angle QPO=90^\circ$,故 $O,B,Q,P,A$ 均在以线段 $OQ$ 为直径的圆周上.
由于 $PN\perp QA,PM\perp QB,PI\perp AB$,所以由Simson定理知:$\triangle QAB$ 的外接圆上一点 $P$ 在其三边的垂足 $N,M,I$ 三点共线,即 $N,M,J,I$ 四点共线.
因为 $QO\perp AB,PI\perp AB$,所以 $QO\parallel PI$,所以 $\angle POQ=\angle IPO$,又因为 $P,A,I,N$ 四点共圆,$P,A,O,Q$ 也四点共圆,所以 $\angle PIJ=\angle PIM=\angle PAN=\angle POQ$.
所以在直角三角形 $PIK$ 中,$\angle PIJ=\angle JPI$,所以 $J$ 为 $PK$ 的中点.因此直线 $MN$ 平分线段 $KP$.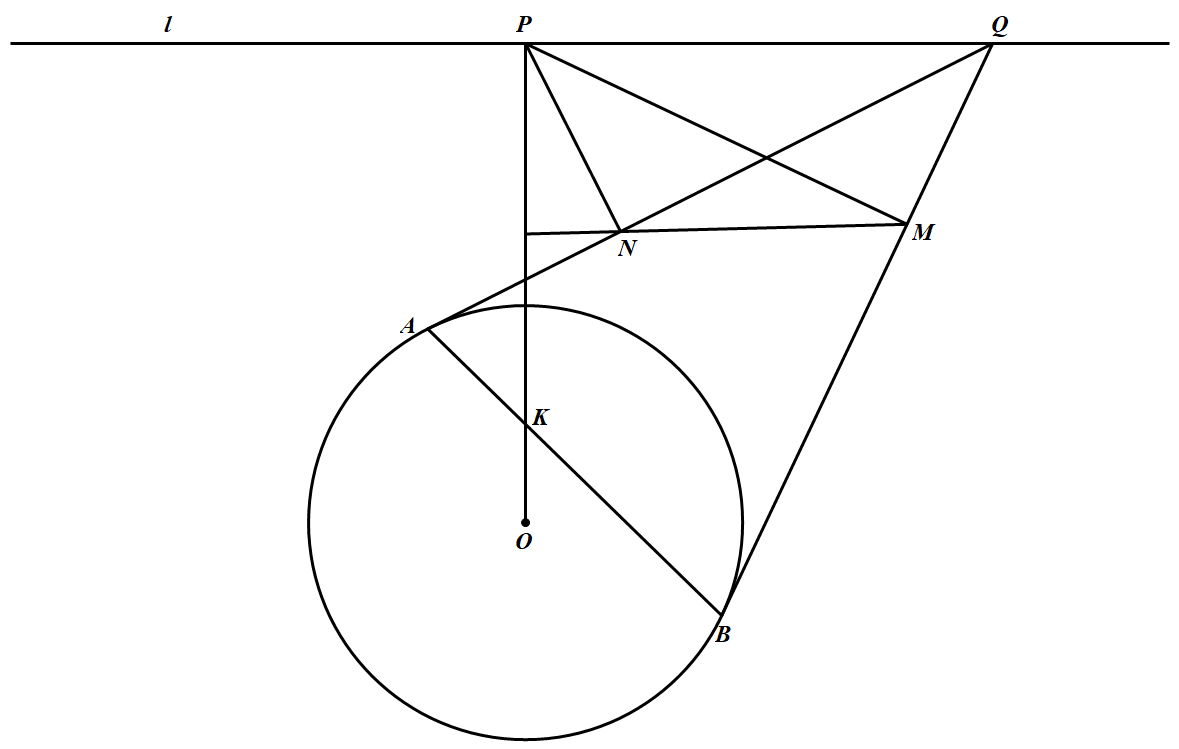
由于 $PN\perp QA,PM\perp QB,PI\perp AB$,所以由Simson定理知:$\triangle QAB$ 的外接圆上一点 $P$ 在其三边的垂足 $N,M,I$ 三点共线,即 $N,M,J,I$ 四点共线.
因为 $QO\perp AB,PI\perp AB$,所以 $QO\parallel PI$,所以 $\angle POQ=\angle IPO$,又因为 $P,A,I,N$ 四点共圆,$P,A,O,Q$ 也四点共圆,所以 $\angle PIJ=\angle PIM=\angle PAN=\angle POQ$.
所以在直角三角形 $PIK$ 中,$\angle PIJ=\angle JPI$,所以 $J$ 为 $PK$ 的中点.因此直线 $MN$ 平分线段 $KP$.

答案
解析
备注