设 $D$ 是 $\triangle ABC$ 的边 $BC$ 上的一点,点 $P$ 在线段 $AD$ 上,过点 $D$ 作一直线分别与线段 $AB,PB$ 交于点 $M,E$,与线段 $AC,PC$ 的延长线交于点 $F,N$.已知 $DE=DF$,求证:$DM=DN$.
【难度】
【出处】
2004中国东南数学奥林匹克试题
【标注】
【答案】
略
【解析】
对 $\triangle AMD$ 和直线 $BEP$ 用梅涅劳斯定理得:$\dfrac{AP}{PD}\cdot\dfrac{DE}{EM}\cdot\dfrac{MB}{BA}=1$ ①
对 $\triangle AFD$ 和直线 $NCP$ 用梅涅劳斯定理得:$\dfrac{AC}{CF}\cdot\dfrac{FN}{ND}\cdot\dfrac{DP}{PA}=1$ ②
对 $\triangle AMF$ 和直线 $BDC$ 用梅涅劳斯定理得:$\dfrac{AB}{BM}\cdot\dfrac{MD}{DF}\cdot\dfrac{FC}{CA}=1$ ③
①②③ 式相乘得:$\dfrac{DE}{EM}\cdot\dfrac{FN}{ND}\cdot\dfrac{MD}{DF}=1$.
又 $DE=DF$,所以有 $\dfrac{DM}{DM-DE}=\dfrac{DN}{DN-DE}$.所以 $DM=DN$.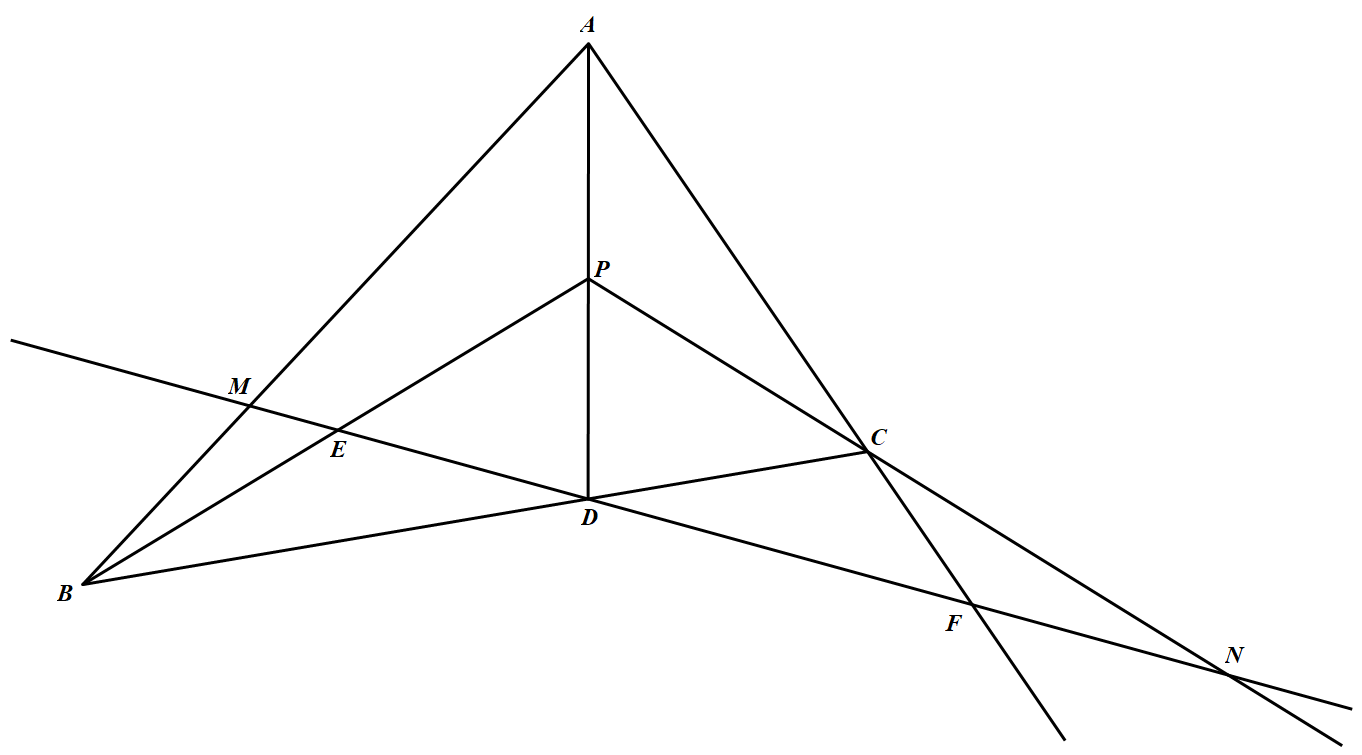
对 $\triangle AFD$ 和直线 $NCP$ 用梅涅劳斯定理得:$\dfrac{AC}{CF}\cdot\dfrac{FN}{ND}\cdot\dfrac{DP}{PA}=1$ ②
对 $\triangle AMF$ 和直线 $BDC$ 用梅涅劳斯定理得:$\dfrac{AB}{BM}\cdot\dfrac{MD}{DF}\cdot\dfrac{FC}{CA}=1$ ③
①②③ 式相乘得:$\dfrac{DE}{EM}\cdot\dfrac{FN}{ND}\cdot\dfrac{MD}{DF}=1$.
又 $DE=DF$,所以有 $\dfrac{DM}{DM-DE}=\dfrac{DN}{DN-DE}$.所以 $DM=DN$.

答案
解析
备注