设圆 $\Gamma$ 是锐角三角形 $ABC$ 的外接圆．点 $D$ 和 $E$ 分别在线段 $AB$ 和 $AC$ 上，满足 $AD=AE$．线段 $BD$ 和 $CE$ 的垂直平分线分别与圆 $\Gamma$ 的劣弧 $\overparen{AB}$ 和 $\overparen{AC}$ 交于点 $F$ 和 $G$．证明：直线 $DE$ 与 $FG$ 平行（或重合）．（希腊）
【难度】
【出处】
2018年第59届IMO试题
【标注】
【答案】
略
【解析】
如图所示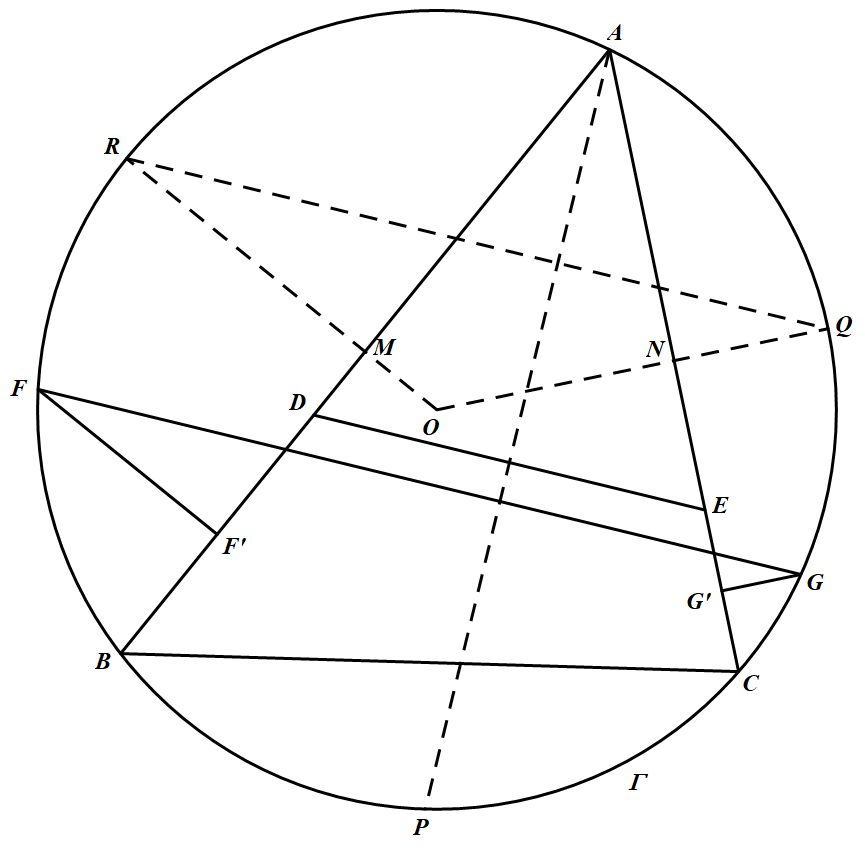
点 $P,Q,R$ 分别是圆 $\Gamma$ 上劣弧 $\overparen{BC},\overparen{CA},\overparen{AB}$ 的中点，点 $M,N$ 分别是线段 $AB,AC$ 的中点，点 $O$ 是 $\Gamma$ 的圆心，于是 $O,M,R$ 共线，$O,N,Q$ 共线．
由 $AD=AE$，$AP$ 平分 $\angle BAC$，可知 $AP\perp DE$．
另一方面 $\dfrac{1}{2}\overparen{AQ}+\dfrac{1}{2}\overparen{PBR}=\dfrac{B}{2}+\dfrac{A+C}{2}=90^\circ$，
故 $QR\perp AP$，从而 $DE\parallel RQ$．只需证明 $FG\parallel RQ$，这等价于 $\overparen{FR}=\overparen{GQ}$．设 $F^\prime,G^\prime$ 分别是线段 $BM,CN$ 的中点，则 $FF^\prime\perp AB,GG^\prime\perp AC$，从而 $FF^\prime\parallel OR,GG^\prime\parallel OQ$．由于
$F^\prime M=BM-BF^\prime =\dfrac{1}{2}(AB-BD)=\dfrac{AD}{2}=\dfrac{AE}{2}=G^\prime N$，
故直线 $FF^\prime$ 与 $GG^\prime $ 分别到圆 $\Gamma$ 的过圆心的直线 $OR$ 与 $OQ$ 的距离相等，故 $\overparen{FR}=\overparen{GQ}$，结论获证．
点 $P,Q,R$ 分别是圆 $\Gamma$ 上劣弧 $\overparen{BC},\overparen{CA},\overparen{AB}$ 的中点，点 $M,N$ 分别是线段 $AB,AC$ 的中点，点 $O$ 是 $\Gamma$ 的圆心，于是 $O,M,R$ 共线，$O,N,Q$ 共线．由 $AD=AE$，$AP$ 平分 $\angle BAC$，可知 $AP\perp DE$．
另一方面 $\dfrac{1}{2}\overparen{AQ}+\dfrac{1}{2}\overparen{PBR}=\dfrac{B}{2}+\dfrac{A+C}{2}=90^\circ$，
故 $QR\perp AP$，从而 $DE\parallel RQ$．只需证明 $FG\parallel RQ$，这等价于 $\overparen{FR}=\overparen{GQ}$．设 $F^\prime,G^\prime$ 分别是线段 $BM,CN$ 的中点，则 $FF^\prime\perp AB,GG^\prime\perp AC$，从而 $FF^\prime\parallel OR,GG^\prime\parallel OQ$．由于
$F^\prime M=BM-BF^\prime =\dfrac{1}{2}(AB-BD)=\dfrac{AD}{2}=\dfrac{AE}{2}=G^\prime N$，
故直线 $FF^\prime$ 与 $GG^\prime $ 分别到圆 $\Gamma$ 的过圆心的直线 $OR$ 与 $OQ$ 的距离相等，故 $\overparen{FR}=\overparen{GQ}$，结论获证．
答案
解析
备注
