设 $R$ 和 $S$ 是圆 $\Omega$ 上互异两点，且 $RS$ 不是直径．设 $l$ 是圆 $\Omega$ 在点 $R$ 处的切线．平面上一点 $T$ 满足，点 $S$ 是线段 $RT$ 的中点．$J$ 是圆 $\Omega$ 的劣弧 $RS$ 上一点，使得三角形 $JST$ 的外接圆 $\Gamma$ 交 $l$ 于两个不同点．记 $\Gamma$ 与 $l$ 的交点中接近 $R$ 的那个为 $A$．直线 $AJ$ 交圆 $\Omega$ 于另一点 $K$．证明：直线 $KT$ 与圆 $\Gamma$ 相切．（卢森堡）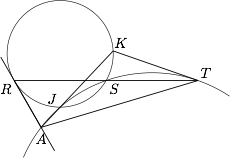
【难度】
【出处】
2017年第58届IMO试题
【标注】
【答案】
略
【解析】
连接 $RK,AS$ 并延长，直线 $RK$ 与 $AS$ 相交于点 $B$，连接 $BT,KS$，如图．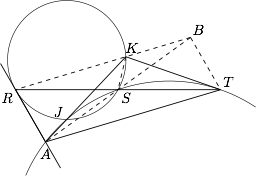
根据题意，有\[\left.\begin{aligned}\left.\begin{aligned}A,J,S,T \text{ 四点共圆}\Rightarrow \angle SJK=\angle ATS\\ R,J,S,K\text{ 四点共圆}\Rightarrow \angle SJK=\angle SRK\end{aligned}\right\}\Rightarrow &RK\parallel AT \\ &RS=ST \end{aligned}\right\}\Rightarrow RATB\text{ 是平行四边形},\]进而\[\left.\begin{aligned}AR\text{ 与 }\Omega \text{ 相切} \Rightarrow \angle SKR=\angle ART\\ RATB\text{ 是平行四边形} \Rightarrow \angle ART=\angle RTB\end{aligned}\right\}\Rightarrow S,K,T,B\text{ 四点共圆}\Rightarrow \angle KTS=\angle KBS,\]又由 $RATB$ 是平行四边形，有 $\angle KBS=\angle SAT$，于是 $\angle KTS=\angle SAT$，根据弦切角定理的逆定理，直线 $KT$ 与圆 $\Gamma$ 相切．
根据题意，有\[\left.\begin{aligned}\left.\begin{aligned}A,J,S,T \text{ 四点共圆}\Rightarrow \angle SJK=\angle ATS\\ R,J,S,K\text{ 四点共圆}\Rightarrow \angle SJK=\angle SRK\end{aligned}\right\}\Rightarrow &RK\parallel AT \\ &RS=ST \end{aligned}\right\}\Rightarrow RATB\text{ 是平行四边形},\]进而\[\left.\begin{aligned}AR\text{ 与 }\Omega \text{ 相切} \Rightarrow \angle SKR=\angle ART\\ RATB\text{ 是平行四边形} \Rightarrow \angle ART=\angle RTB\end{aligned}\right\}\Rightarrow S,K,T,B\text{ 四点共圆}\Rightarrow \angle KTS=\angle KBS,\]又由 $RATB$ 是平行四边形，有 $\angle KBS=\angle SAT$，于是 $\angle KTS=\angle SAT$，根据弦切角定理的逆定理，直线 $KT$ 与圆 $\Gamma$ 相切．
答案
解析
备注
