已知三角形 $BCF$ 中，角 $B$ 是直角，在直线 $CF$ 上取点 $A$，使得 $FA=FB$，且 $F$ 在点 $A$ 和 $C$ 之间．取点 $D$，使得 $DA=DC$，且 $AC$ 是 $\angle DAB$ 的内角平分线．取点 $E$，使得 $EA=ED$，且 $AD$ 是 $\angle EAC$ 的内角平分线．设 $M$ 是线段 $CF$ 的中点，取点 $X$ 使得 $AMXE$ 是一个平行四边形（这里 $AM\parallel EX$，$AE\parallel MX$）．证明：直线 $BD$、$FX$ 和 $ME$ 三线共点。（比利时）
【难度】
【出处】
2016年第57届IMO试题
【标注】
【答案】
略
【解析】
如图所示．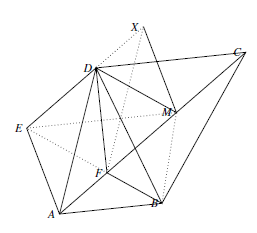
由条件，我们有 $\angle FAB=\angle FBA=\angle DAC=\angle DCA=\angle EAD=\angle EDA$，记为 $\theta$．
由于 $\triangle ABF\sim\triangle ACD$，有 $\frac{AB}{AC}=\frac{AF}{AD}$，于是 $\triangle ABC\sim\triangle AFD$．又 $EA=ED$，有
$\angle AFD=\angle ABC=90^{\circ}+\theta=180^{\circ}-\frac{1}{2}\angle AED$
于是 $F$ 在以 $E$ 为圆心，$EA$ 为半径的圆周上，特别地，$EF=EA=ED$，再由
$\angle EFA=\angle EAF=2\theta=\angle BFC$
可知 $B,F,E$ 共线．
由于 $\angle EDA=\angle MAD$，因此 $ED\parallel AM$，从而 $E,D,X$ 共线．
由 $M$ 是直角三角形 $CBF$ 斜边 $CF$ 的中点可得，$MF=MB$．
在等腰三角形 $EFA$ 和 $MFB$ 中，
$\angle EFA=\angle MFB,~AF=BF$
因此它们全等，从而 $BM=AE=XM$
且 $BE=BF+FE=AF+FM=AM=EX$
从而 $\triangle EMB\cong\triangle EMX$．
又由于 $EF=ED$，$D,F$ 关于 $EM$ 对称，$X,B$ 也关于 $EM$ 对称，从而直线 $BD$ 和 $XF$ 关于 $EM$ 对称．
由此即得 $BD,FX,ME$ 三线共点．
由条件，我们有 $\angle FAB=\angle FBA=\angle DAC=\angle DCA=\angle EAD=\angle EDA$，记为 $\theta$．由于 $\triangle ABF\sim\triangle ACD$，有 $\frac{AB}{AC}=\frac{AF}{AD}$，于是 $\triangle ABC\sim\triangle AFD$．又 $EA=ED$，有
$\angle AFD=\angle ABC=90^{\circ}+\theta=180^{\circ}-\frac{1}{2}\angle AED$
于是 $F$ 在以 $E$ 为圆心，$EA$ 为半径的圆周上，特别地，$EF=EA=ED$，再由
$\angle EFA=\angle EAF=2\theta=\angle BFC$
可知 $B,F,E$ 共线．
由于 $\angle EDA=\angle MAD$，因此 $ED\parallel AM$，从而 $E,D,X$ 共线．
由 $M$ 是直角三角形 $CBF$ 斜边 $CF$ 的中点可得，$MF=MB$．
在等腰三角形 $EFA$ 和 $MFB$ 中，
$\angle EFA=\angle MFB,~AF=BF$
因此它们全等，从而 $BM=AE=XM$
且 $BE=BF+FE=AF+FM=AM=EX$
从而 $\triangle EMB\cong\triangle EMX$．
又由于 $EF=ED$，$D,F$ 关于 $EM$ 对称，$X,B$ 也关于 $EM$ 对称，从而直线 $BD$ 和 $XF$ 关于 $EM$ 对称．
由此即得 $BD,FX,ME$ 三线共点．
答案
解析
备注
