在三角形 $ABC$ 中，$\Omega$ 是其外接圆，$O$ 是其外心．以 $A$ 为圆心的一个圆 $\Gamma$ 与线段 $BC$ 交于两点 $D$ 和 $E$，使得 $B,D,E,C$ 互不相同，并且按此顺序排列在直线 $BC$ 上．设 $F$ 和 $G$ 是 $\Gamma$ 和 $\Omega$ 的两个交点，并且使得点 $A,F,B,C,G$ 按此顺序排列在 $\Omega$ 上．设 $K$ 是三角形 $BDF$ 的外接圆和线段 $AB$ 的另一个交点．设 $L$ 是三角形 $CGE$ 的外接圆和线段 $CA$ 的另一个交点．假设直线 $FK$ 和 $GL$ 不相同，且相交于点 $X$．
证明：$X$ 在直线 $AO$ 上．（希腊）
证明：$X$ 在直线 $AO$ 上．（希腊）
【难度】
【出处】
2015年第56届IMO试题
【标注】
【答案】
略
【解析】
如图所示．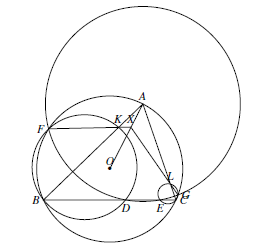
由于 $AF=AG$，而 $AO$ 是 $\angle FAG$ 的内角平分线，故 $F,G$ 关于直线 $AO$ 对称．要证明点 $X$ 在直线 $AO$ 上，只需证明
$\angle AFK=\angle AGL$
首先
$\angle AFK=\angle DFG+\angle GFA-\angle DFK$
由 $D,F,G,E$ 共圆，有 $\angle DFG=\angle CEG$．由 $A,F,B,G$ 共圆，有 $\angle GFA=\angle GBA$．由 $D,B,F,K$ 共圆，有 $\angle DFK=\angle DBK$．从而
$\angle AFK=\angle CEG+\angle GBA-\angle DBK=\angle CEG-\angle CBG$
再由 $C,E,L,G$ 共圆，得 $\angle CEG=\angle CLG$．由 $C,B,A,G$ 共圆，有 $\angle CBG=\angle CAG$．故
$\angle AFK=\angle CLG-\angle CAG=\angle AGL$
结论获证．
由于 $AF=AG$，而 $AO$ 是 $\angle FAG$ 的内角平分线，故 $F,G$ 关于直线 $AO$ 对称．要证明点 $X$ 在直线 $AO$ 上，只需证明$\angle AFK=\angle AGL$
首先
$\angle AFK=\angle DFG+\angle GFA-\angle DFK$
由 $D,F,G,E$ 共圆，有 $\angle DFG=\angle CEG$．由 $A,F,B,G$ 共圆，有 $\angle GFA=\angle GBA$．由 $D,B,F,K$ 共圆，有 $\angle DFK=\angle DBK$．从而
$\angle AFK=\angle CEG+\angle GBA-\angle DBK=\angle CEG-\angle CBG$
再由 $C,E,L,G$ 共圆，得 $\angle CEG=\angle CLG$．由 $C,B,A,G$ 共圆，有 $\angle CBG=\angle CAG$．故
$\angle AFK=\angle CLG-\angle CAG=\angle AGL$
结论获证．
答案
解析
备注
