2014年第55届IMO试题

• 知识点

  >

  二试几何部分

略

证法一
设过点 $C$ 且垂直于直线 $SC$ 的直线和直线 $AB$ 交于点 $Q$（如图），则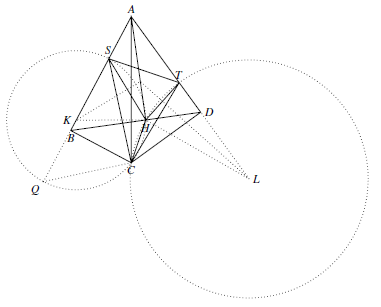$\angle SQC=90^{\circ}-\angle BSC=180^{\circ}-\angle SHC$
因此 $C,H,S,Q$ 四点共圆．由于 $SQ$ 为此圆直径，所以三角形 $SHC$ 的外心 $K$ 在 $AB$ 上，同理，三角形 $CHT$ 的外心 $L$ 在 $AD$ 上．
要证明 $BD$ 与三角形 $SHT$ 的外接圆相切，只需证明 $HS$ 和 $HT$ 的中垂线的交点在 $AH$ 上，而上述两条线段的中垂线恰好为 $\angle AKH$ 和 $\angle ALH$ 的角平分线，由内角平分线定理，只需证明
$\frac{A K}{K H}=\frac{A L}{L H}$ ①
即可．
下面我们给出 ① 的两种证明：
证明一：设直线 $KL$ 与直线 $HC$ 交于点 $M$．因为 $KH=KC, LH=LC$，所以点 $H$ 和 $C$ 关于直线 $KL$ 对称，因此 $M$ 为 $HC$ 的中点．设 $O$ 为四边形 $ABCD$ 的外接圆圆心，因此 $O$ 为 $AC$ 中点．故我们有 $OM\parallel AH$，因而 $OM\perp BD$．结合 $OB=OD$ 知，$OM$ 为 $BD$ 的中垂线，因此 $BM=DM$．
因为 $CM\perp KL$，所以 $B,C,M,K$ 四点共圆，且以 $KC$ 为育径．同理，$L,C,M,D$ 四点共圆，且以 $LC$ 为直径．这样，由正弦定理可得
$
\dfrac{A K}{A L}=\dfrac{\sin \angle A L K}{\sin \angle A K L}=\dfrac{D M}{C L} \cdot \dfrac{C K}{B M}=\dfrac{C K}{C L}=\dfrac{K H}{L H}
$
即知 ① 式成立，命题得证．
证明二：如果 $A,H$ 和 $C$ 三点共线，那么 $AK=AL,KH=LH$，这样 ① 式就成立．所以我们下面假设 $A,H$ 和 $C$ 三点不共线，考虑过这三点的圆 $\omega$．因为四边形 $ABCD$ 是圆内接四边形，所以
$
\angle B A C=\angle B D C=90^{\circ}-\angle A D H=\angle A H D
$
设 $N\neq A$ 是圆 $\omega$ 和 $\angle CAH$ 的平分线的另一个交点．那么 $AN$ 也是 $\angle BAD$ 的角平分线．又由于 $H$ 和 $C$ 关于直线 $KL$ 对称，且 $HN=NC$，我们知道 $N$ 和圆 $\omega$ 的中心都在直线 $KL$ 上．
这就说明圆 $\omega$ 是点 $K$ 和 $L$ 的一个Apollonius圆，由此即得 ①．
证法二
延长 $CB$ 至 $E$，使得 $CB=BE$．延长 $OD$ 至 $F$，使得 $CD=DF$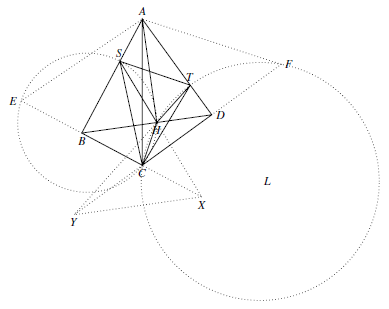．连结图中线段．这样 $AB$ 垂直平分 $CE$，$AD$ 垂直平分 $CF$．从而有 $CS=ES, CT=FT$，且 $A$ 是 $\triangle CEF$ 的外心．
因为 $BD\parallel EF$，$AH\perp BD$，所以 $AH\perp EF$，这样 $AH$ 垂直平分 $EF$，从而 $HE=HF$．
又由于
$
\angle C H S=90^{\circ}+\angle B S C=180^{\circ}-\angle S C B=180^{\circ}-\angle S E B
$
所以 $S,E,C,H$ 四点共圆，从而有
$X H \cdot X S=X C \cdot X E$ ②
同时，由 $CS=ES$ 且 $S,H$ 在 $CE$ 同侧，可知 $SH$ 是 $\angle CHE$ 的外角平分线．
类似地，由于
$
\angle C H T=90^{\circ}+\angle D T C=180^{\circ}-\angle T C D=180^{\circ}-\angle T F D
$
所以 $T,F,C,H$ 四点共圆，从而有
$Y C \cdot Y F=Y H \cdot Y T$ ③
同时，由 $CT=FT$ 且 $T,H$ 在 $CF$ 同侧，可知 $TH$ 是 $\angle CHT$ 的外角平分线．
根据题意，$C,H$ 在 $AB$ 同侧，所以 $CH<EH=FH$．
设 $X$ 为直线 $EC$ 和直线 $SH$ 的交点，$Y$ 为直线 $FC$ 和直线 $TH$ 的交点，则 $X$ 在线段 $EC$ 的延长线上，$Y$ 在线段 $FC$ 的延长线上．由外角平分线定理可知
$
\dfrac{C X}{X E}=\dfrac{C H}{H E}=\dfrac{C H}{H F}=\dfrac{C Y}{Y F}
$
所以 $XY\parallel EF$，从而 $XY \perp AH$．
又由 ②，③ 可知直线 $XY$ 即为 $\triangle CEF$ 的外接圆和 $\triangle TSH$ 的外接圆（记其外心为 $O$）
的根轴．于是 $XY\perp AO$，所以 $A,O,H$ 三点共线．于是 $OH\perp XY,OH\perp BD$．所以 $BD$ 是 $\bigodot O$ 在 $H$ 点处的切线．证毕．
证法三
设 $\angle THA=\alpha,\angle DAH=\beta$，设 $AH=a,BH=b,DH=d,DT=x$．延长 $TH$ 和 $DC$ 交于 $L$．在 $AH$ 上取点 $M$，使得 $MT\perp TH$；在 $AH$ 上取点 $N$，使得 $NS \perp SH$．作 $TR \perp AH$ 于 $R$，作 $MU\perp AD$ 于 $U$，作 $HV\perp AD$ 于 $V$．下证 $M=N$．
由 $\angle DAH=\beta$ 知 $\angle ADH=90^{\circ}-\beta,\angle BDC=\beta$．而同时我们有 $\angle ABD=\angle ACD,\angle AHB=\angle ADC$，所以 $\triangle ADC\sim\triangle AHB$，所以 $DC=b\cdot\frac{\sqrt{a^2 + d^2}}{a}$，这样
$
T C^{2}=T D^{2}+D C^{2}=x^{2}+\dfrac{b^{2}\left(a^{2}+d^{2}\right)}{a^{2}}
$
由张角定理知 $\dfrac{1}{d}=\dfrac{\cos \beta}{D L}+\dfrac{\sin \beta}{x}$，所以 $D L=\dfrac{x d \cos \beta}{x-d \sin \beta}$．
由余弦定理知 $T H^{2}=x^{2}+d^{2}-2 x d \sin \beta$，而
$
\dfrac{T L}{T H}=\dfrac{D L}{D H \sin \left(90^{\circ}-\beta\right)}=\dfrac{x}{x-d \sin \beta}
$
所以
$\begin{aligned} T L \cdot T H &=\frac{T L}{T H} \cdot T H^{2} =\left(x^{2}+d^{2}-2 x d \sin \beta\right) \frac{x}{x-d \sin \beta} \end{aligned}$
而因为 $\angle THC-\angle DTC=90^{\circ}$，即有 $\angle THC=\angle TCL$，所以 $TC^2 =TL\cdot TH$，即
$
x^{2}+\dfrac{b^{2}\left(a^{2}+d^{2}\right)}{a^{2}}=\left(x^{2}+d^{2}-2 x d \sin \beta\right) \dfrac{x}{x-d \sin \beta}
$
整理得
$x^{2}+\dfrac{b^{2}\left(a^{2}+d^{2}\right)-a^{2} d^{2}}{a^{2} d \sin \beta} x-\dfrac{b^{2}\left(a^{2}+d^{2}\right)}{a^{2}}=0$ ④
解得
$x=\dfrac{a^{2} d^{2}-a^{2} b^{2}-b^{2} d^{2}+\sqrt{k}}{2 a^{2} d \sin \beta}$ ⑤
（由 $T$ 在 $AD$ 上，可知应取正根），其中
$
k=a^{4} b^{4}+b^{4} d^{4}+a^{4} d^{4}+2 a^{2} b^{4} d^{2}+2 a^{2} b^{2} d^{4}-2 a^{4} b^{2} d^{2}
$
我们注意到 $k$ 的表达式关于 $b,d$ 是对称的．
$\begin{aligned} \tan \alpha &=\frac{T R}{R H}=\frac{\left(\sqrt{a^{2}+d^{2}}-x\right) d}{a x} \\ \tan (\alpha+\beta) &=\frac{D L}{D T}=\frac{\frac{x d \cos \beta}{x-d \cos \beta}}{x}=\frac{d \cos \beta}{x-d \cos \beta} \end{aligned}$
$\begin{aligned} \frac{A M}{A H}=\frac{M U}{H V} &=\frac{M U}{T V} \cdot \frac{T V}{V H}=\frac{M T}{T H} \cdot \frac{T V}{V H}=\frac{\tan \alpha}{\tan (\alpha+\beta)} \\ &=\frac{(x-d \sin \beta)\left(\sqrt{a^{2}+d^{2}}-x\right)}{a x \cos \beta} \\ &=\frac{\left(\sqrt{a^{2}+d^{2}}-x\right)\left(\sqrt{a^{2}+d^{2}} x-d^{2}\right)}{a^{2} x} \\ &=\frac{1}{a^{2}}\left(-\sqrt{a^{2}+d^{2}} x-\frac{d^{2} \sqrt{a^{2}+d^{2}}}{x}+a^{2}+2 d^{2}\right) \end{aligned}$
由 ④ 式，
$
\dfrac{1}{x}=\dfrac{a^{2}}{a^{2} b^{2}+b^{2} d^{2}} x+\dfrac{a^{2} b^{2}+b^{2} d^{2}-a^{2} d^{2}}{\left(a^{2} b^{2}+b^{2} d^{2}\right) d \sin \beta}
$
代入知
$\begin{aligned} \frac{A M}{A H}=& \frac{1}{a^{2}}\left(-\frac{a^{2} b^{2}+b^{2} d^{2}+a^{2} d^{2}}{a^{2} b^{2}+b^{2} d^{2}} \sqrt{a^{2}+d^{2}} x-\right.\\ & \frac{a^{2} b^{2}+b^{2} d^{2}-a^{2} d^{2}}{b^{2}}+a^{2}+2 d^{2} ) \end{aligned}$
结合 ⑤ 可知
$\begin{aligned} \frac{A M}{A H}=& \frac{1}{a^{2}}\left(-\left(a^{2} b^{2}+b^{2} d^{2}+a^{2} d^{2}\right) \frac{\sqrt{k}}{2 a^{2} b^{2} d^{2}}+\right.\\ & \frac{a^{4} d^{4}+a^{4} b^{4}+b^{4} d^{4}+2 a^{2} b^{4} b^{2}+2 a^{2} b^{2} d^{4}}{2 a^{2} b^{2} d^{2}} \end{aligned}$
已知 $\dfrac{AM}{AH}$ 关于 $b,d$ 对称，所以 $\dfrac{AM}{AH}=\dfrac{AN}{AH}$，即 $M=N$．所以 $M,S,A,H,T$ 共圆，它们的外心在 $AH$ 上，且 $AH\perp BD$．所以直线 $BD$ 和三角形 $TSH$ 的外接圆外切．